
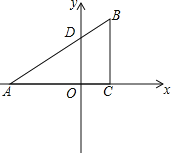
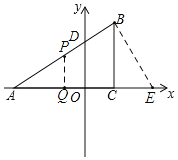
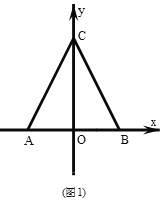
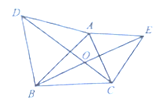
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЪЧжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЕуAЁЂCЕФКсзјБъЪЧвЛдЊЖўДЮЗНГЬx2+2x-3=0ЕФСНИљЃЈAOЃОOCЃЉЃЌжБЯпABгыyжсНЛгкDЃЌDЕуЕФзјБъЮЊ![]()
ЃЈ1ЃЉЧѓжБЯпABЕФКЏЪ§БэДяЪНЃЛ
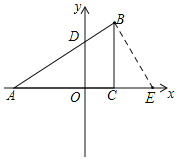
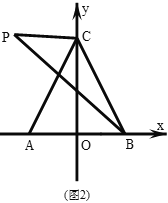
ЃЈ2ЃЉдкxжсЩЯеввЛЕуEЃЌСЌНгEBЃЌЪЙЕУвдЕуAЁЂEЁЂBЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЈВЛАќРЈШЋЕШЃЉЃЌВЂЧѓЕуEЕФзјБъЃЛ
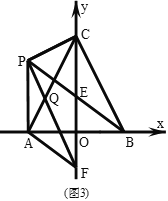
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуPЁЂQЗжБ№ЪЧABКЭAEЩЯЕФЖЏЕуЃЌСЌНгPQЃЌЕуPЁЂQЗжБ№ДгAЁЂEЭЌЪБГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕБЕуPЕНДяЕуBЪБЃЌСНЕуЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЮЪМИУыЪБвдЕуAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAEBЯрЫЦЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ![]() ЃЌ0ЃЉЃЈ2ЃЉy=
ЃЌ0ЃЉЃЈ2ЃЉy=![]() x+
x+![]() ЃЈ3ЃЉt=
ЃЈ3ЃЉt=![]() ЪБвдЕуAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAEBЯрЫЦ
ЪБвдЕуAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAEBЯрЫЦ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩЧѓЕуAЃЌЕуCЕФзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпABЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЧѓЕуBЕФзјБъЃЌМДПЩЧѓACЃЌBCЃЌABЕФГЄЃЌгЩRtЁїABCЁзRtЁїAEBЃЌПЩЕУ![]() ЃЌПЩЧѓAEЕФГЄЃЌМДПЩЧѓЕуEЕФзјБъЃЛ
ЃЌПЩЧѓAEЕФГЄЃЌМДПЩЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉЗжЁїAPQЁзЁїABEЃЌЁїAPQЁзЁїAEBСНжжЧщПіЬжТлЃЌПЩЧѓtЕФжЕЃЎ
Нт:ЁпЕуAЁЂCЕФКсзјБъЪЧвЛдЊЖўДЮЗНГЬx2+2x-3=0ЕФСНИљ
ЁрЕуAЁЂCЕФКсзјБъЗжБ№ЮЊ-3ЃЌ1
ЁрЕуAЃЈ-3ЃЌ0ЃЉЃЌЕуCЃЈ1ЃЌ0ЃЉ
ЩшжБЯпABНтЮіЪНЃКy=kx+![]() ЃЌЧвЙ§ЕуA
ЃЌЧвЙ§ЕуA
Ёр0=-3k+![]()
Ёрk=![]()
ЁржБЯпABНтЮіЪНЃКy=![]() x+
x+![]()
ЃЈ2ЃЉШчЭМЃКЙ§BзїBEЁЭABНЛxжсгкEЃЌ
ЕБx=1ЪБЃЌдђy=![]() +
+![]() =3
=3
ЁрЕуBЃЈ1ЃЌ3ЃЉ
ЁрAC=4ЃЌBC=3
ЁрAB=5
ЁпRtЁїABCЁзRtЁїAEB
Ёр![]()
Ёр![]()
ЁрAE=![]()
ЁрOE=![]() -3=
-3=![]()
ЁрЕуEЃЈ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ЃЈ3ЃЉгЩЬтвтПЩЕУЃКAP=tЃЌAQ=![]() -t
-t
ШчЭМЃК
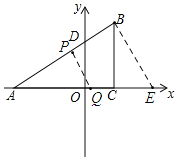
ШєЁїAPQЁзЁїABE
Ёр![]()
Ёр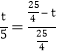
Ёрt=![]()
ШчЭМЃК
ШєЁїAPQЁзЁїAEB
Ёр![]()
Ёр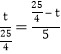
Ёрt=![]()
злЩЯЫљЪіЃКt=![]() ЪБвдЕуAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAEBЯрЫЦЃЎ
ЪБвдЕуAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAEBЯрЫЦЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌЧвОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌдђЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк2aЉbЃН0ЃЛЂлaЃМЉ![]() ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
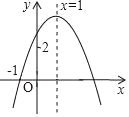
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
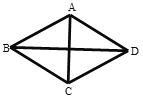
ЁОЬтФПЁПШчЭМЃЌдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌвбжЊЁїABCЕФжмГЄЮЊ15ЃЌдђСтаЮ
ЃЌвбжЊЁїABCЕФжмГЄЮЊ15ЃЌдђСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЕФГЄЮЊ( ).
ЕФГЄЮЊ( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌжБЯп
ЮЊзјБъдЕуЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсИКАыжсКЭ
жсИКАыжсКЭ![]() жсе§Аыжсгк
жсе§Аыжсгк![]() СНЕуЃЌНЋ
СНЕуЃЌНЋ![]() би
би![]() жсЗелжС
жсЗелжС![]() ЃЌЧв
ЃЌЧв![]() ЕФУцЛ§ЮЊ8.
ЕФУцЛ§ЮЊ8.
(1)ШчЭМЃЌЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
(2)ШчЭМЃЌЕу![]() ЮЊЕкЖўЯѓЯоФк
ЮЊЕкЖўЯѓЯоФк![]() ЩЯЗНЕФвЛЕуЃЌСЌНг
ЩЯЗНЕФвЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪН(гУКЌ
ЕФКЏЪ§ЙиЯЕЪН(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
(3)ШчЭМЃЌдк(2)ЕФЬѕМўЯТЃЌСЌНг![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсИКАыжсЩЯвЛЕуЃЌ
жсИКАыжсЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() зјБъ.
зјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃГѕШ§вЛДЮФЃФтПМЪдКѓЃЌЪ§бЇРЯЪІАбвЛАрЕФЪ§бЇГЩМЈжЦГЩШчЭМЫљЪОВЛЭъећЕФЭГМЦЭМ(ТњЗж120ЗжЃЌУПзщКЌзюЕЭЗжЃЌВЛКЌзюИпЗж)ЃЌВЂИјГіШчЯТаХЯЂЃКЂйЕкЖўзщЦЕТЪЪЧ![]() ЃЛЂкЕкЖўЁЂШ§зщЕФЦЕТЪКЭЪЧ
ЃЛЂкЕкЖўЁЂШ§зщЕФЦЕТЪКЭЪЧ![]() ЃЛЂлздзѓжСгвЕкШ§ЁЂЫФЁЂЮхзщЕФЦЕЪ§БШЮЊ
ЃЛЂлздзѓжСгвЕкШ§ЁЂЫФЁЂЮхзщЕФЦЕЪ§БШЮЊ![]() .ЧыФуНсКЯЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
.ЧыФуНсКЯЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
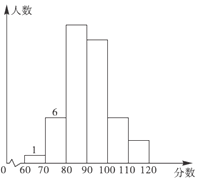
(1)ШЋАрбЇЩњЙВга______ШЫЃЌЕкШ§зщЕФШЫЪ§ЮЊ______ШЫЃЛ
(2)ШчЙћГЩМЈВЛЩйгк![]() ЗжЮЊгХауЃЌФЧУДШЋФъМЖ
ЗжЮЊгХауЃЌФЧУДШЋФъМЖ![]() ШЫжаГЩМЈДяЕНгХауЕФДѓдМЖрЩйШЫЃП
ШЫжаГЩМЈДяЕНгХауЕФДѓдМЖрЩйШЫЃП
(3)ШєВЛЩйгк![]() ЗжЕФбЇЩњПЩвдЛёЕУбЇаЃАфЗЂЕФНБзДЃЌЧвУПАрбЁХЩСНУћДњБэдкбЇаЃаТбЇЦкПЊбЇЪНжаСьНБЃЌдђИУАрЕУЕН
ЗжЕФбЇЩњПЩвдЛёЕУбЇаЃАфЗЂЕФНБзДЃЌЧвУПАрбЁХЩСНУћДњБэдкбЇаЃаТбЇЦкПЊбЇЪНжаСьНБЃЌдђИУАрЕУЕН![]() ЗжЕФаЁЧПЭЌбЇФмБЛбЁжаСьНБЕФИХТЪЪЧЖрЩйЃП
ЗжЕФаЁЧПЭЌбЇФмБЛбЁжаСьНБЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЗжБ№вд
жаЃЌЗжБ№вд![]() ЃЌ
ЃЌ![]() ЮЊБпЯђ
ЮЊБпЯђ![]() ЭтзїЕШБп
ЭтзїЕШБп![]() КЭЕШБп
КЭЕШБп![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊЃК____________________.
ЕФЖШЪ§ЮЊЃК____________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊБпГЄзїЕШБп
ЮЊБпГЄзїЕШБп![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЦНаагк
ЦНаагк![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊБпГЄзїЕШБп
ЮЊБпГЄзїЕШБп![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЦНаагк
ЦНаагк![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊБпГЄзїЕШБп
ЮЊБпГЄзїЕШБп![]() ЃЌЁЃЌдђЕШБп
ЃЌЁЃЌдђЕШБп![]() ЕФБпГЄЪЧ______.
ЕФБпГЄЪЧ______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊКыбяжаЛЊДЋЭГЮФЛЏЃЌФГаЃзщжЏЦпФъМЖ800УћбЇЩњВЮМгЪЋДЪДѓШќЃЌЮЊСЫНтбЇЩњећЬхЕФЪЋДЪЛ§РлЧщПіЃЌЫцЛњГщШЁВПЗжбЇЩњЕФГЩМЈ(ЕУЗжШЁе§ећЪ§ЃЌТњЗжЮЊ100Зж)НјааЭГМЦЗжЮіЃЌЧыИљОнЩаЮДЭъГЩЕФСаЭМБэЃЌНтД№ЮЪЬтЃК
зщБ№ | ЗжЪ§ЖЮ | ЦЕЪ§ | ЦЕТЪ |
вЛ | 50.5ЁЋ60.5 | 16 | 0.08 |
Жў | 60.5ЁЋ70.5 | 40 | 0.20 |
Ш§ | 70.5ЁЋ80.5 | 50 | 0.25 |
ЫФ | 80.5ЁЋ90.5 | m | 0.35 |
Юх | 90.5ЁЋ100.5 | 24 | n |
(1)БОДЮГщбљжаЃЌБэжаm=____ЃЌn=____ЃЌбљБОГЩМЈЕФжаЮЛЪ§ТфдкЕк____зщФкЃЎ
(2)ВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЎ
(3)ШєЙцЖЈГЩМЈГЌЙ§80ЗжЮЊгХауЃЌЧыЙРМЦИУаЃЦпФъМЖбЇЩњжаЪЋДЪЛ§РлГЩМЈЮЊгХауЕФШЫЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com