
已知:在直角坐标系中,E为第二象限内一点,⊙E与x轴自左至右交于A、B两点,直线PC切⊙E于C,交x轴于P,D为线段PC上一点,ED⊥BC,已知PB=2,△PBD的周长为![]() 。
。
(1)求证:DB是⊙E的切线;
(2)若抛物线![]() 经过A、B两点,求m的值;
经过A、B两点,求m的值;
(3)在过P点的直线中,是否存在这样的直线,该直线与(2)中的抛物线的两个交点的横坐标之和等于2?若存在,求出这样的直线的解析式;若不存在,请说明理由。
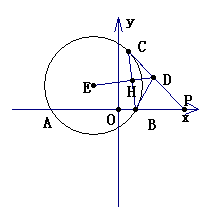
(1)证:连结EC、EB,
∵PC切⊙E于C, ∴∠ECP=90°,
∵EC=EB,EH=EH ∵ED⊥BC于H,
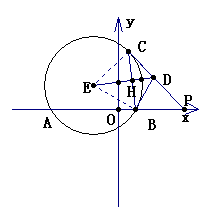
∴△CEH≌△BEH, ∴∠CEH=∠BEH,
∴△CED≌△BED, ∴∠ECD=∠EBD=90°,
∴BD是⊙E的切线, ∴BD=DC。
(2)∵△PBD的周长为![]() ,PB=2,
,PB=2,
∴![]() ∴
∴![]() ,
,
∵PC切⊙E于C,PBA为⊙E的割线,
∴PC2=PB?PA ∴12=2?PA ∴PA=6, ∴AB=4
∵抛物线![]() 与x轴交于A(x1,0),B(x2,0),x1<0,x2>0,
与x轴交于A(x1,0),B(x2,0),x1<0,x2>0,
∴x1+x2=-2,x1x2=-4m<0m>0,
∵AB=4,
∴![]()
![]()
![]()
∴4=1+4m ∴![]() ∴
∴![]() 。
。
(3)令y=0
∴x1=-3, x2=1
∴A(-3,0),B(1,0)
∵PB=2, ∴P(3,0)
设过P(3,0)的直线为y=kx-3k。
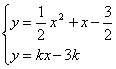
∴![]()
∴x2+2(1-k)x-3+6k=0
设抛物线与直线的交点的横坐标为x3,x4,
∴x3+x4=2(k-1)
x3-x4=6k-3
依题意:x3+x4=2
∴2(k-1)=2 ∴k=2,
当k=2时,Δ=4(1-k)2-4(6k-3)
=4-4×9<0
∴不存在这样的直线。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
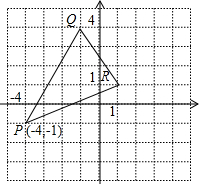 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com