
【题目】已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,连接CE.
(1)发现问题
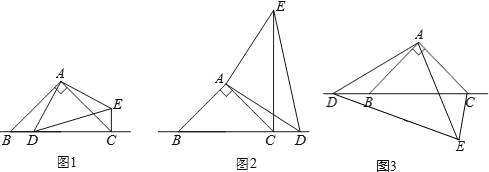
如图①,当点D在边BC上时,
①请写出BD和CE之间的数量关系为________,位置关系为________;
②线段CE+CD=________AC;
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;
(3)拓展延伸
如图③,当点D在边CB的延长线上且其他条件不变时,若BC=4,CE=2,求线段CD的长.
【答案】(1)①BD=CE,BD⊥CE;②![]() ;(2)成立,理由见解析;(3)6.
;(2)成立,理由见解析;(3)6.
【解析】
试题分析:(1)证明:如图1中,①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵AD=AE,∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,∠ABC=∠ACE=45°,∴∠ECB=90°,∴BD⊥CE;
,∴△ABD≌△ACE,∴BD=CE,∠ABC=∠ACE=45°,∴∠ECB=90°,∴BD⊥CE;

②结论:CE+CE=![]() AC.理由:由①得BD=CE,∴BC=
AC.理由:由①得BD=CE,∴BC=![]() AC,∵BC=BD+CD=CE+CD,∴CE+CD=
AC,∵BC=BD+CD=CE+CD,∴CE+CD=![]() AC;
AC;
(2)解:如图2中,存在数量关系为:CE=![]() AC+CD;
AC+CD;
理由:由(1)同理可得在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,在等腰直角三角形ABC中,BC=
,∴△ABD≌△ACE,∴BD=CE,在等腰直角三角形ABC中,BC=![]() AC,∴BD=BC+CD=
AC,∴BD=BC+CD=![]() AC+CD,∴CE=
AC+CD,∴CE=![]() AC+CD;
AC+CD;

(3)解:由(1)同理在△ABD与△ACE中, ,∴△ABD≌△ACE,∴BD=CE,∴CD=BC+BD=BC+CE.∵BC=4,CE=2,∴CD=6.
,∴△ABD≌△ACE,∴BD=CE,∴CD=BC+BD=BC+CE.∵BC=4,CE=2,∴CD=6.



科目:初中数学 来源: 题型:
【题目】“若|a|>1,则a>1”是一个假命题,可以用举反例的方法说明它是假命题,下列选项中恰当的反例是( )
A.a=5B.a=﹣5C.a=1D.a=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列问题中,两个变量间的函数关系式是反比例函数的是
A. 小颖每分钟可以制作2朵花,x分钟可以制作y朵花
B. 体积为10cm3的长方体,高为hcm,底面积为Scm2
C. 用一根长50cm的铁丝弯成一个矩形,一边长为xcm,面积为Scm2
D. 汽车油箱中共有油50升,设平均每天用油5升,x天后油箱中剩下的油量为y升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“淄博地区明天降水概率是15%”,下列说法中,正确的是
A. 淄博地区明天降水的可能性较小
B. 淄博地区明天将有15%的时间降水
C. 淄博地区明天将有15%的地区降水
D. 淄博地区明天肯定不降水
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是南海中学八年级(15)班的40名学生的出生月份的调查记录:
![]()
(1)请你重新设计一张统计表,使全班同学在每个月出生人数情况一目了然;
(2)求出10月份出生的学生的频数和频率;
(3)现在是1月份,如果你准备为下个月生日的每一位同学送一份小礼物,那你应该准备多少份礼物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元一次方程 x2﹣8x﹣4=0,经配方后得到的方程是( )
A. (x﹣4)2=20 B. (x﹣4)2=16 C. (x﹣4)2=12 D. (x﹣4)2=4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com