
【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2 ![]() =(1+
=(1+ ![]() )2 , 我们来进行以下的探索:
)2 , 我们来进行以下的探索:
设a+b ![]() =(m+n
=(m+n ![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b ![]() =m2+2n2+2mn
=m2+2n2+2mn ![]() ,∴a=m+2n2 , b=2mn
,∴a=m+2n2 , b=2mn
, 这样就得出了把类似a+b ![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b ![]() =(m﹣n
=(m﹣n ![]() )2 , 用含m,n的式子分别表示a,b,得a= , b=;
)2 , 用含m,n的式子分别表示a,b,得a= , b=;
(2)利用上述方法,找一组正整数a,b,m,n填空:﹣ ![]() =(﹣
=(﹣ ![]() )2
)2
(3)a﹣4 ![]() =(m﹣n
=(m﹣n ![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
【答案】
(1)m2+5n2|2mn
(2)9|4|2|1
(3)解:∵2mn=4,
∴mn=2,
而m,n都为正整数,
∴m=2,n=1或m=1,n=2,
当m=2,n=1时,a=9;
当m=1,n=2时,a=21.
即a的值为9或21
【解析】解:(1)∵a﹣b ![]() =(m﹣n
=(m﹣n ![]() )2,
)2,
∴a﹣b ![]() =m2﹣2
=m2﹣2 ![]() mn+5n2,
mn+5n2,
∴a=m2+5n2,n=2mn;
2)取m=2,n=1,
则a=4+5=9,b=4;
故答案为m2+5n2,2mn;9,4,2,1.
(1)利用完全平方公式把(m﹣n ![]() )2展开即可得到用含m,n的式子分别表示出a,b;(2)利用(1)中的表达式,令m=2,n=1,则可计算出对应的a和b的值;(3)利用(1)的结果得到2mn=4,则mn=2,再利用m,n都为正整数得到m=2,n=1或m=1,n=2,然后计算对应的a的值即可.
)2展开即可得到用含m,n的式子分别表示出a,b;(2)利用(1)中的表达式,令m=2,n=1,则可计算出对应的a和b的值;(3)利用(1)的结果得到2mn=4,则mn=2,再利用m,n都为正整数得到m=2,n=1或m=1,n=2,然后计算对应的a的值即可.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】(阅读材料)
小明同学遇到下列问题:
解方程组 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y,
这时原方程组化为 ,解得
,解得![]() ,
,
把![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得![]() 解得
解得![]() .
.
所以,原方程组的解为![]()
(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 ;
;
(2)已知方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的一点,
边上的一点,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着边
出发,以每秒1个单位的速度沿着边![]() 向终点
向终点![]() 运动,连接
运动,连接![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)当![]() 为多少秒时,
为多少秒时,![]() 是直角三角形?
是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,给出以下结论:①
,给出以下结论:①![]() 为等腰直角三角形;②
为等腰直角三角形;②![]() 为等边三角形;③
为等边三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(立方米)之间关系的图象如图所示,根据图象回答:
(1)该市自来水收费,每户用水不超过5立方米时,每立方米收费多少元?超过5立方米时,超过的部分每立方米收费多少元?
(2)求出y与x之间的关系式.
(3)若某户居民某月用水量为3.5立方米,则应交水费多少元?若某户居民某月交水费17元,则该户居民用水多少立方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
A.7
B.11
C.13
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
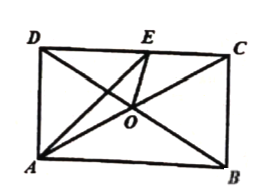
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com