
【题目】两个反比例函数y= ![]() (k>1)和y=
(k>1)和y= ![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= ![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y= ![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y= ![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y= ![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号) 
【答案】①③④
【解析】解:设点P的坐标为(m, ![]() ),则点A(m,
),则点A(m, ![]() ),点C(m,0),点B(
),点C(m,0),点B( ![]() ,
, ![]() ),点D(0,
),点D(0, ![]() ), ∴PB=m﹣
), ∴PB=m﹣ ![]() =
= ![]() ,PD=m,PA=
,PD=m,PA= ![]() ﹣
﹣ ![]() =
= ![]() ,PD=m,PC=
,PD=m,PC= ![]() ,
,
∵ ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴BA∥DC,①成立;
∵PB= ![]() ,PA=
,PA= ![]() ,
,
∴当m2=k时,PA=PB,②不成立;
S矩形OCPD=k,S△OBD= ![]() ,S△OAC=
,S△OAC= ![]() ,
,
S四边形PAOB=S矩形OCPD﹣S△OBD﹣S△OBD=k﹣1,
∵k为固定值,
∴③成立;
S梯形BECA= ![]() (AC+BE)EC=
(AC+BE)EC= ![]() (
( ![]() +
+ ![]() )(m﹣
)(m﹣ ![]() )=
)= ![]() ,S△OBA=S四边形PAOB
,S△OBA=S四边形PAOB![]() (m﹣
(m﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=
)= ![]() ,
,
∴S梯形BECA=S△OBA , ④成立.
综上可知:一定正确的为①③④.
所以答案是:①③④.
【考点精析】本题主要考查了反比例函数的性质和比例系数k的几何意义的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知A,B是线段EF上两点,EA:AB:BF=1:2:3,M,N分别为EA,BF的中点,且MN=8cm,则EF长( ) ![]()
A.9cm
B.10cm
C.11cm
D.12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 ![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.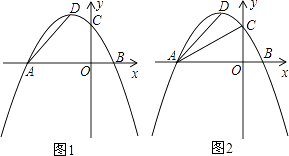
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y= ![]() (k>1)和y=
(k>1)和y= ![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= ![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y= ![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y= ![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y= ![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m,n是正实数,且满足m+n=mn时,就称点P(m, ![]() )为“完美点”,已知点A(0,5)与点M都在直线y=-x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=
)为“完美点”,已知点A(0,5)与点M都在直线y=-x+b上,点B,C是“完美点”,且点B在线段AM上,若MC= ![]() ,AM=4
,AM=4 ![]() ,求△MBC的面积.
,求△MBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com