
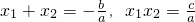 .借助该材料完成下列各题:
.借助该材料完成下列各题: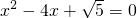 的两个实数根,x1+x2=______;x1•x2=______.
的两个实数根,x1+x2=______;x1•x2=______. =______;
=______; =______.
=______.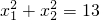 ,求m的值.
,求m的值.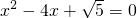 的两个实数根,
的两个实数根, =4,x1•x2=
=4,x1•x2=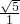 =
= ;
; ;
;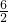 =3,x1•x2=
=3,x1•x2=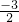 =-
=- ,
, =
=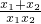 =
=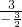 =-2,
=-2, =(x1+x2)2-2x1•x2=32-2×(-
=(x1+x2)2-2x1•x2=32-2×(- )=12.
)=12. ,或m≤5-4
,或m≤5-4
 =(x1+x2)2-2x1•x2=13,即(m-3)2-2(m+8)=13,
=(x1+x2)2-2x1•x2=13,即(m-3)2-2(m+8)=13,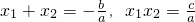 ,来解题.
,来解题.

科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,x1x2=
,x1x2= .∵
.∵
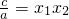 ,∴
,∴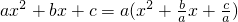 =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
查看答案和解析>>
科目:初中数学 来源:四川省月考题 题型:解答题
 ,x1x2=
,x1x2= .
.
 ,
, =a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).
=a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).查看答案和解析>>
科目:初中数学 来源:2010-2011学年四川省内江市隆昌三中九年级(上)第一次月考数学试卷(解析版) 题型:解答题
 ,x1x2=
,x1x2= .∵
.∵
 ,∴
,∴ =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com