
【题目】观察下列等式:
2+22=23﹣2;
2+22+23=24﹣2;
2+22+23+24=25﹣2;
2+22+23+24+25=26﹣2;
…
已知按一定规律排列的一组数:220,221,222,223,224,…,238,239,240,若220=m,则220+221+222+223+224+…+238+239+240=_____(结果用含m的代数式表示).
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
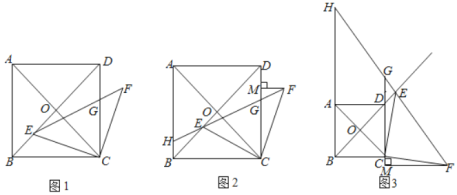
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,线段![]() 的延长线交
的延长线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 为射线
为射线![]() 上一点,线段
上一点,线段![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,请直接写出线段
,请直接写出线段![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
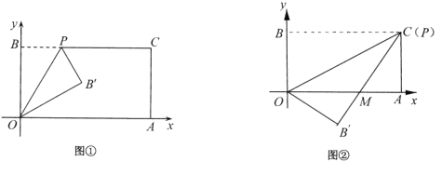
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
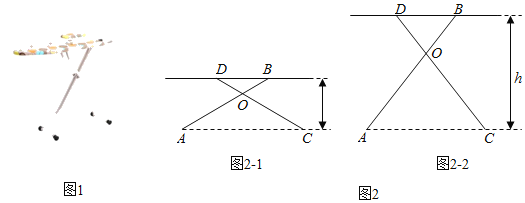
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
(1)求AB的长;
(2)求证:四边形ACED是菱形;
(3)设点C的坐标为(0,![]() ),△ECD与△AOB重合部分的面积为
),△ECD与△AOB重合部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
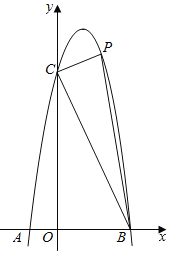
【题目】如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“新冠肺炎”的发生,市场上防护口罩出现热销.某药店第一次用2000元购进若干个防护口罩,并按定价2.5元/个出售,很快售完由于该防护口罩畅销,第二次购进时,每个防护口罩的进价比第一次的进价提高了25%,该药店用3000元购进防护口罩的数量比第一次多了200个,并把定价提高20%进行销售.
(1)第一次购进时,每个防护口罩的价格是多少元?
(2)第二次售出800个防护口罩时,出现了滞销,该药店打算降价售完剩余的防护口罩.那么该药店每个防护口罩至多降价多少元出售,才能使第二次销售的防护口罩不亏本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com