练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    填空题．

    (1)在同一平面内，______的两条直线叫做平行线．

    (2)经过直线外一点，______条直线与这条直线平行．

    (3)如果两条直线都与第三条直线平行，那么这两条直线______．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    17、说理题：
    阅读并完成填空：
    如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE．
    （1）△BCD与△EAB是否全等？为什么？
    解：∵DC⊥CA，EA⊥CA，DB⊥EB（已知）
    ∴∠C=∠A=∠DBE=90°（
    已知
    ）
    ∵∠1+∠DBE+∠2=180°
    ∴∠1+∠2=90°
    又∵∠1+∠D+∠C=180°（　　）
    ∴∠1+∠D=90°
    ∴∠D=
    ∠2
    （同角的余角相等）
    在△BCD与△EAB中
    ∠C=
    ∠A
    （已证）
    ∠D
    =
    ∠2
    （已证）
    DB=
    BE
    （已知）
    ∴△BCD≌△EAB（
    AAS
    ）
    （2）你能利用（1）中所证得的结论说明AC=CD+AE吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    说理题：
    阅读并完成填空：
    如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE．
    （1）△BCD与△EAB是否全等？为什么？
    解：∵DC⊥CA，EA⊥CA，DB⊥EB（已知）
    ∴∠C=∠A=∠DBE=90°（______）
    ∵∠1+∠DBE+∠2=180°
    ∴∠1+∠2=90°
    又∵∠1+∠D+∠C=180°
    ∴∠1+∠D=90°
    ∴∠D=______（同角的余角相等）
    在△BCD与△EAB中
    ∠C=______（已证）
    ______=______（已证）
    DB=______（已知）
    ∴△BCD≌△EAB（______）
    （2）你能利用（1）中所证得的结论说明AC=CD+AE吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

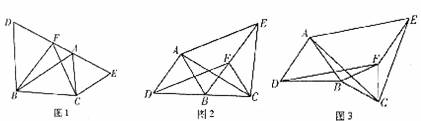
    如图1，点D、F、A、E在同一直线上，且AE=DF，分别以DA、AE为一边，在直线DE

    的同侧作等边△DBA和等边△ACE，试证明△BCF也是等边三角形。

    （1）下面是小伟对此题的分析过程，请你根据他的分析填空：此题中，要想证明△BCF是等边三角形，至少要证明两条边相等。欲证两条边相等，可以通过证明这两条边所在的两个三角形全等来实现。根据已知条件，在不加辅助线的情况下，不妨尝试证明       ≌△ABC，依据是                 （写出定义、公理或定理的内容）；

    （2）如图2，点D、B、C在同一直线上，分别以DB、BC为一边，在直线DC的同侧作等边△DBA和等边△BCF，再以DA、DF为邻边作□ADFE，求证：△ACE是等边三角形；

    （3）如图3是将（2）中的等边△BCF绕点B顺时针旋转一个角度后得到的图形，若其他条件不变，△ACE是否还是等边三角形?请加以说明。

    查看答案和解析>>

    同步练习册答案