
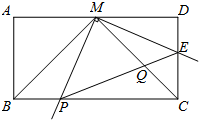
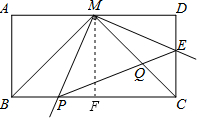
 (2012•郑州模拟)如图,在矩形ABCD中,点M是AD的中点,AD=4
(2012•郑州模拟)如图,在矩形ABCD中,点M是AD的中点,AD=4| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•郑州模拟)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,若∠1=26°,则∠2的度数为
(2012•郑州模拟)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,若∠1=26°,则∠2的度数为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•郑州模拟)郑州地铁一号线将于2013年底建成,它的通车将给市民的出行方式带来一些新变化.小王和小林准备利用课余时间,以问卷的方式对郑州市民的出行方式进行调查.如图是郑州地铁一号线图(部分),小王和小林分别从郑州火车站、二七广场站、市体育馆站这三站中,随机选取一站向其周围的人群进行问卷调查,则小王选取的站点与小林选取的站点相邻的概率是
(2012•郑州模拟)郑州地铁一号线将于2013年底建成,它的通车将给市民的出行方式带来一些新变化.小王和小林准备利用课余时间,以问卷的方式对郑州市民的出行方式进行调查.如图是郑州地铁一号线图(部分),小王和小林分别从郑州火车站、二七广场站、市体育馆站这三站中,随机选取一站向其周围的人群进行问卷调查,则小王选取的站点与小林选取的站点相邻的概率是| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•郑州模拟)已知二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.
(2012•郑州模拟)已知二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com