
如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B⇒A,B⇒C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.
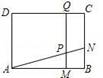
(1)若a=4厘米,t=1秒,则PM= _________ 厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.
(1)PM=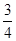 ;(2)当t=2时,使△PNB∽△PAD,相似比为2:3;(3)3<a≤6;(4)∵3<a≤6时,当a=2
;(2)当t=2时,使△PNB∽△PAD,相似比为2:3;(3)3<a≤6;(4)∵3<a≤6时,当a=2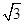 时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
【解析】
试题分析:(1)要想求出PM的长度,可以利用△ANB∽△APM得到比例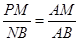 ,当t=1时,MB=1,NB=1,AM=3,∴PM=
,当t=1时,MB=1,NB=1,AM=3,∴PM=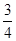 ;(2)当△PNB∽△PAD时,可以得到比例
;(2)当△PNB∽△PAD时,可以得到比例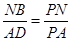 ,∵△ANB∽△APM, ∴
,∵△ANB∽△APM, ∴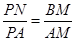 ,∴
,∴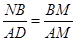 ,可以求出t;(3)要判断两个梯形的面积是否相等,只需要把各自的面积表示出来,得到方程,方程有解,则存在,由题,△AMP∽△ABN,∴
,可以求出t;(3)要判断两个梯形的面积是否相等,只需要把各自的面积表示出来,得到方程,方程有解,则存在,由题,△AMP∽△ABN,∴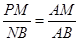 ,即
,即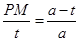 ,∴PM=
,∴PM=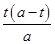 ,∵PQ=3﹣
,∵PQ=3﹣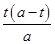 ,当梯形PMBN与梯形PQDA的面积相等,即
,当梯形PMBN与梯形PQDA的面积相等,即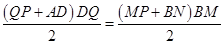 ,化简得t=
,化简得t= ,∵t≤3,∴3<a≤6;(4)由(2)知道,当3<a≤6时,梯形PMBN与梯形PQDA的面积相等,∴梯形PQCN的面积与梯形PMBN的面积相等即可,将两个梯形的面积表示出来,得到方程,方程有解,则a存在,则CN=PM,∴
,∵t≤3,∴3<a≤6;(4)由(2)知道,当3<a≤6时,梯形PMBN与梯形PQDA的面积相等,∴梯形PQCN的面积与梯形PMBN的面积相等即可,将两个梯形的面积表示出来,得到方程,方程有解,则a存在,则CN=PM,∴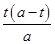 =3﹣t,得t2﹣2at+3a=0,把t=
=3﹣t,得t2﹣2at+3a=0,把t= 代入,得9a3﹣108a=0,∵a≠0,∴9a2﹣108=0,∴a=±2
代入,得9a3﹣108a=0,∵a≠0,∴9a2﹣108=0,∴a=±2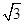 ,∴a=2
,∴a=2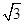 ,当a=2
,当a=2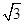 时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
试题解析:(1)当t=1时,MB=1,NB=1,AM=4﹣1=3,
∵PM∥BN,
∴△ANB∽△APM,
∴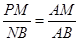 ,
,
∴PM=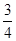 ;
;
(2)由题,∵△PNB∽△PAD,
∴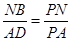 ,
,
∵△ANB∽△APM,
∴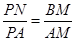 ,
,
∴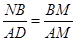 ,
,
∴t=2,相似比为2:3;
(3)∵PM⊥AB,CB⊥AB,∠AMP=∠ABC,
∴△AMP∽△ABN,
∴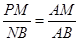 ,即
,即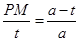 ,
,
∴PM=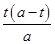 ,
,
∵PQ=3﹣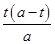 ,
,
当梯形PMBN与梯形PQDA的面积相等,即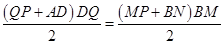 =
=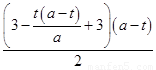 =
=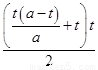 ,
,
化简得t= ,
,
∵t≤3,
∴ ≤3,
≤3,
则a≤6,
∴3<a≤6;
(4)由(2)知道,当3<a≤6时,梯形PMBN与梯形PQDA的面积相等,
∴梯形PQCN的面积与梯形PMBN的面积相等即可,则CN=PM,
∴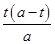 =3﹣t,
=3﹣t,
两边同时乘以a,得at﹣t2=3a﹣at,
整理,得t2﹣2at+3a=0,
把t= 代入,整理得9a3﹣108a=0,
代入,整理得9a3﹣108a=0,
∵a≠0,
∴9a2﹣108=0,
∴a=±2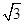 ,
,
∴a=2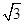 ,
,
∴存在a,当a=2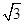 时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
时梯形PMBN与梯形PQDA的面积、梯形PQCN的面积相等.
考点:1.三角形的相似;2.一元二次方程;3.不等式.


科目:初中数学 来源: 题型:
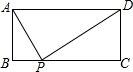 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com