
【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
【答案】(l)200;(2)见解析;(3)144o;(4)![]()
【解析】
(1)由最喜欢跳绳运动的人数及其所占百分比可得总人数;
(2)根据各组人数之和等于总人数求得最喜欢投篮运动的人数,再除以总人数可得其对应百分比,从而补全图1和图2;
(3)用360°乘以最喜欢跳绳运动的人数所占百分比可得跳绳所在的扇形圆心角的度数;
(4)总人数乘以样本中最喜欢跳绳运动的人数所占百分比即可得.
解:(1)被调查的学生总人数为80÷40%=200,
故答案为:200;
(2)最喜欢投篮运动的人数为200-(40+80+20)=60,
最喜欢投篮运动的人数所占百分比为![]() ×100%=30%,
×100%=30%,
补全图形如下: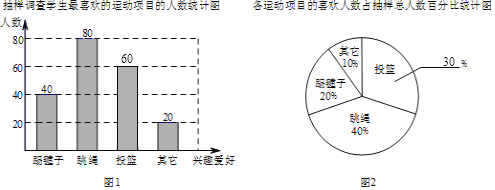
(3)图2中跳绳所在的扇形对应的圆心角的度数是为360°×40%=144°.
故答案为144°;
(4)2400×40%=960(人).
答:估计全校学生中最喜欢跳绳运动的人数约为960人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(2016四川省攀枝花市)某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,试说明∠EDF=∠A.

解:∵DF∥AB ( ),
∴∠A+∠AFD=180° ( ).
∵DE∥AC ( ),
∴∠AFD+∠EDF=180° ( ).
∴∠A=∠EDF ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中k为常数,且
(其中k为常数,且![]() ),则称点
),则称点![]() 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:![]() 的“4属派生点”为
的“4属派生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“2属派生点”
的“2属派生点”![]() 的坐标为________;
的坐标为________;
(2)若点P的“3属派生点”![]() 的坐标为
的坐标为![]() ,求点P的坐标;
,求点P的坐标;
(3)若点P在y轴的正半轴上,点P的“k属派生点”为![]() 点,且点
点,且点![]() 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
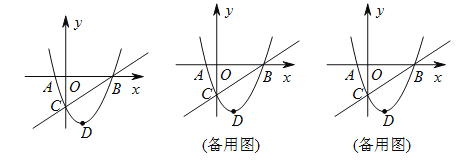
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线顶点,点
是抛物线顶点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(![]() )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
(![]() )连结
)连结![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )当四边形
)当四边形![]() 的面积最大时,求出此时
的面积最大时,求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
(![]() )若把条件“点
)若把条件“点![]() 是直线
是直线![]() 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点![]() 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com