
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平
的平
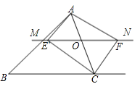
分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?为什么?
是矩形?为什么?
![]() 进行怎样的变化才能使
进行怎样的变化才能使![]() 边上存在点
边上存在点![]() ,使四边形
,使四边形![]() 是正方形?为什么?
是正方形?为什么?
【答案】(1)见解析;(2)当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,理由见解析
是矩形,理由见解析
【解析】
(1)由已知MN∥BC得到两对内错角相等,再由CE、CF分别平分∠BCO和∠GCO,根据等量代换可推出∠OEC=∠OCE,∠OFC=∠OCF,分别根据“等角对等边”得证;
(2)由(1)得出的EO=CO=FO,点O运动到AC的中点时,则由EO=CO=FO=AO,根据对角线互相平分且相等的四边形为矩形得证;
(3)由已知和(2)得到的结论,点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,则推出四边形AECF是矩形且对角线垂直,所以四边形AECF是正方形.
![]() 证明:∵
证明:∵![]() ,
,
∴![]() ,
,![]() ,
,
又已知![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
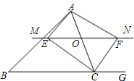
![]() 解:当点
解:当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形.
是矩形.
∵当点![]() 运动到
运动到![]() 的中点时,
的中点时,![]() ,又
,又![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
又![]() 为
为![]() 的平分线,
的平分线,![]() 为
为![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴四边形![]() 是矩形;
是矩形;![]() 解:当点
解:当点![]() 运动到
运动到![]() 的中点时,且
的中点时,且![]() 满足
满足![]() 为直角的直角三角形时,四边形
为直角的直角三角形时,四边形![]() 是正方形.
是正方形.
∵由![]() 知,当点
知,当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,
是矩形,
已知![]() ,当
,当![]() ,则
,则
![]() ,
,
∴![]() ,
,
∴四边形![]() 是正方形.
是正方形.


科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到
年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到![]() 年比
年比![]() 年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少?
年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列短文,回答有关问题:
在实数这章中,遇到过![]() 、
、![]() ;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用
;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用![]() 将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,例如,
将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,例如,![]() 化成最简二次根式是
化成最简二次根式是![]() ,
,![]() 化成最简二次根式是
化成最简二次根式是![]() .几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
.几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
![]() 请判断下列各式中,哪些是同类二次根式?
请判断下列各式中,哪些是同类二次根式?![]() ;
;
![]() 二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:
二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:矩形
,求证:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
![]() 当线段
当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,直接写出
时,直接写出![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,AC的延长线上有点D,AC=3CD,连接BD,E为BD的中点,CE是⊙O的切线.
(1)求证:BD与⊙O相切;
(2)求∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现,
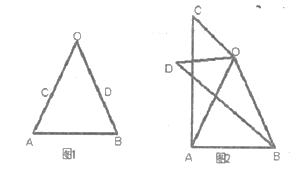
如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,将点
上一点,将点![]() 绕点
绕点![]() 顺时针旋转50°得到点
顺时针旋转50°得到点![]() ,则
,则![]() 与
与![]() 的数量关系是________________________。
的数量关系是________________________。
(2)类比探究
如图2,将(1)中的![]() 绕点
绕点![]() 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
(3)拓展延伸
![]() 绕点
绕点![]() 在平面旋转,当旋转到
在平面旋转,当旋转到![]() 时,请直接写出
时,请直接写出![]() 度数。
度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com