
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() ;(4)的坐标为:
;(4)的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把A、C两点坐标代入抛物线解析式可求得a、c的值,可求得抛物线解析;
(2)可求得点C关于x轴的对称点C′的坐标,连接C′N交x轴于点K,再求得直线C′K的解析式,可求得K点坐标;
(3)过点E作EG⊥x轴于点G,设Q(m,0),可表示出AB、BQ,再证明△BQE≌△BAC,可表示出EG,可得出△CQE关于m的解析式,再根据二次函数的性质可求得Q点的坐标;
(4)分DO=DF、FO=FD和OD=OF三种情况,分别根据等腰三角形的性质求得F点的坐标,进一步求得P点坐标即可.
![]() ∵抛物线经过点
∵抛物线经过点![]() ,
,![]() ,
,
∴![]() ,解得
,解得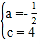 ,
,
∴抛物线解析式为![]() ;
;
![]() 由
由![]() 可求得抛物线顶点为
可求得抛物线顶点为![]() ,
,
如图![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() 点即为所求,
点即为所求,
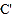
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 、
、![]() 点坐标代入可得
点坐标代入可得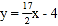 ,解得
,解得 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
![]() 设点
设点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图
,如图![]() ,
,
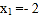
由![]() ,得
,得![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
∴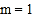 .
.
又∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时
,此时![]() ;
;
![]() 存在.在
存在.在![]() 中,
中,
![]() 若
若![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() .
.
又在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
此时,点![]() 的坐标为
的坐标为![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
此时,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
![]() 若
若![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
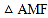
由等腰三角形的性质得:![]() ,
,
∴![]() .
.
∴在等腰直角![]() 中,
中,![]() .
.
∴![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
此时,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
![]() 若
若![]() ,
,
∵![]() ,且
,且![]() .
.
∴![]() .
.
∴点![]() 到
到![]() 的距离为
的距离为![]() .
.
而![]() ,与
,与![]() 矛盾.
矛盾.
∴在![]() 上不存在点使得
上不存在点使得![]() .
.
此时,不存在这样的直线![]() ,使得
,使得![]() 是等腰三角形.
是等腰三角形.
综上所述,存在这样的直线![]() ,使得
,使得![]() 是等腰三角形.所求点
是等腰三角形.所求点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣![]() ) C. (﹣
) C. (﹣![]() ,﹣2
,﹣2![]() ﹣1) D. (﹣
﹣1) D. (﹣![]() ,﹣2
,﹣2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内部一点,∠APB,∠BPC,∠CPA的大小之比是5:6:7,则以PA、PB、PC为边的三角形的三个内角的大小之比是(从小到大)( )
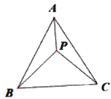
A.2:3:4B.4:5:6C.3:4:5D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足![]() .
.
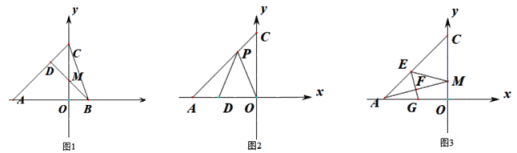
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3![]() ,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A.y![]() ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a![]() +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3
C.x(x﹣1)=x![]() ﹣xD.m
﹣xD.m![]() +n
+n![]() =(m+n)(m﹣n)
=(m+n)(m﹣n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com