
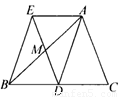
如图,已知AD是△ABC的边BC上的中线,△BME是△AMD绕点M按顺时针方向旋转180°得到的,连结AE,求证:DE=AC.
见解析
【解析】
试题分析:由旋转可得△BME≌△AMD,即可证得四边形AEBD是平行四边形,从而得到AE=BD,AE∥BD,再有BD=CD,即可得到四边形AEDC是平行四边形,问题得证.
∵△BME是△AMD绕点M按顺时针方向旋转180°得到的,
∴△BME≌△AMD,
∴BE=AD,∠EBM=∠DAM,
∴BE∥AD,
∴四边形AEBD是平行四边形,
∴AE=BD,AE∥BD,
∵BD=CD,
∴AE=CD,
∴四边形AEDC是平行四边形,
∴DE=AC
考点:本题考查的是旋转的性质,平行四边形的判定和性质
点评:解答本题的关键是熟练掌握平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
 9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )
9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:
18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com