
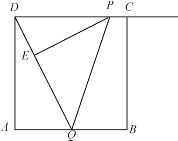
【题目】如图,正方形ABCD,点P为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.
(1)请找出图中一对相似三角形,并证明;
(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.
【答案】(1)△DPE∽△QDA,证明见解析;(2)DP=2或5
【解析】
(1)由∠ADC=∠DEP=∠A=90![]() 可证明△ADQ∽△EPD;
可证明△ADQ∽△EPD;
(2)若以点P,E,Q为顶点的三角形与△ADQ相似,有两种情况,当△ADQ∽△EPQ时,设EQ=x,则EP=2x,则DE=2![]() x,由△ADQ∽△EPD可得
x,由△ADQ∽△EPD可得![]() ,可求出x的值,则DP可求出;同理当△ADQ∽△EQP时,设EQ=2a,则EP=a,可得
,可求出x的值,则DP可求出;同理当△ADQ∽△EQP时,设EQ=2a,则EP=a,可得![]() ,可求出a的值,则DP可求.
,可求出a的值,则DP可求.
(1)△ADQ∽△EPD,证明如下:
∵PE⊥DQ,
∴∠DEP=∠A=90![]() ,
,
∵∠ADC=90![]() ,
,
∴∠ADQ+∠EDP=90![]() ,∠EDP+∠DPE=90
,∠EDP+∠DPE=90![]() ,
,
∴∠ADQ=∠DPE,
∴△ADQ∽△EPD;
(2)∵AB=4,点Q为AB的中点,
∴AQ=BQ=2,
∴DQ=![]() ,
,
∵∠PEQ=∠A=90![]() ,
,
∴若以点P,E,Q为顶点的三角形与△ADQ相似,有两种情况,
①当△ADQ∽△EPQ时,![]() ,
,
设EQ=x,则EP=2x,则DE=2![]() x,
x,
由(1)知△ADQ∽△EPD,
∴![]() ,
,
∴![]() ,
,
∴x=![]()
∴DP=![]() =5;
=5;
②当△ADQ∽△EQP时,设EQ=2a,则EP=a,
同理可得![]() ,
,
∴a=![]() ,
,
DP=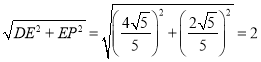 .
.
综合以上可得DP长为2或5,使得以点P,E,Q为顶点的三角形与△ADQ相似.


科目:初中数学 来源: 题型:
【题目】 某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图,如图所示:
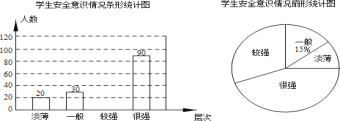
根据以上信息,解答下列问题:
(1)这次调查一共抽取了______名学生,将条形统计图补充完整;
(2)扇形统计图中,“较强”层次所占圆心角的大小为______°;
(3)若该校有3200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 的图象上位于直线
的图象上位于直线![]() 下方的点,过点
下方的点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() ,交直线
,交直线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
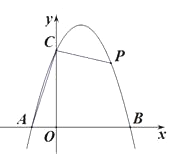
(1)抛物线的解析式为________;
(2)P为抛物线上一点,连结AC,PC,若∠PCO=3∠ACO,点P的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)试问△OBC与△ABD全等吗?并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由;
(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m
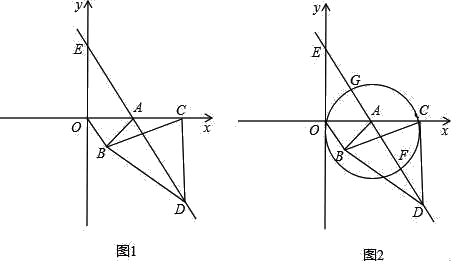
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com