证明:(1)∵四边形ADEF是正方形,
∴AD=AF,∠FAD=90°=∠BAC,
∴∠FAD-∠DAC=∠BAC-∠DAC,
∴∠FAC=∠BAD,
在△ABD和△ACF中
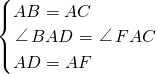
,
∴△ABD≌△ACF(SAS),
∴∠B=∠FCA,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠ACF=90°,
∴FC⊥BC.

(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD=AC,
∴AC=CF,
∴∠CAF=∠CFA,
∵四边形ADEF是正方形,
∴AD=EF,∠DAF=∠EFA=90°,
∴∠DAF-∠CAF=∠EFA-∠CFA,
∴∠DAC=∠EFC,
在△DAC和△EFC中

,
∴△DAC≌△EFC(SAS),
∴CD=CE.
分析:(1)根据正方形的性质得出AD=AF,∠FAD=90°=∠BAC,求出∠FAC=∠BAD,证出△ABD≌△ACF,推出∠B=∠FCA即可;
(2)根据△ABD≌△ACF,推出BD=CF=AC,求出∠DAC=∠EFC,根据SAS推出△DAC≌△EFC即可.
点评:本题考查了正方形性质,全等三角形的性质和判定,等腰直角三角形性质的应用,主要考查学生综合运用定理进行推理的能力.

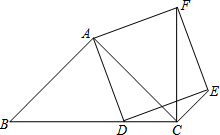 如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE.
如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE.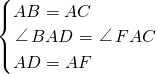 ,
,
 ,
,

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案