
已知,△ABC为等边三角形,点P是射线CM上一点,连接AP,把△ACP绕点A按顺时针方向旋转60°,得△ABD,直线BD与射线CM交于点E,连接AE.
(1)如图,①求∠BEC的度数;
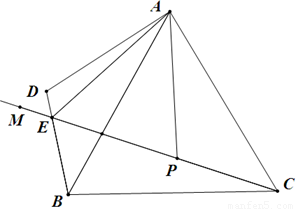
②若AE=2BE,猜想线段CE、BE的数量关系,并证明你的猜想;
(2)如图,若AE=mBE,求 的值.
的值.
见试题解析.
【解析】
试题分析:⑴  为等边三角形,点
为等边三角形,点 是射线
是射线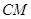 上一点,连接
上一点,连接 ,把△ACP绕点A按顺时针方向旋转60°,得
,把△ACP绕点A按顺时针方向旋转60°,得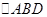 ,旋
,旋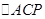 转得到
转得到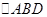 ,所以
,所以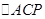 ≌
≌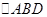 ,根据角的关系可得
,根据角的关系可得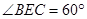
⑵再由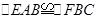 得到
得到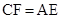 ,已知
,已知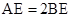 所以
所以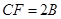 即可得.
即可得. 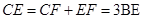 .
.
⑶有(2)证明可知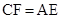 ,因为
,因为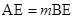 所以
所以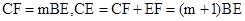 ,即可得
,即可得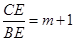
试题解析:.(1)∵∵△ACP旋转得到△ABD
∴△ACP≌△ABD
∴∠ACP=∠ABD 1分
∵△ABC是等边三角形
∴∠ABC=∠ACB=60°
∵∠BCP+∠ACP=∠ACB
∴∠BCP+∠ABD=∠ACB=60°
∵∠BCP+∠ABD+∠ABC+∠BEC=180°
∴∠BEC=60° 2分
(2) CE=3BE 3分
在EC上截取EF=EB,连结BF
∵∠BEC=60°, EF=EB
∴△BEF是等边三角形
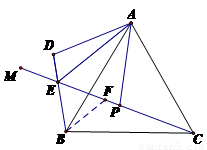
∴∠EBF=60°,EF=EB=BF 4分
∵△ABC是等边三角形
∴∠ABC=60°,AB=BC
∵∠EBF-∠ABF=∠EBA, ∠ABC-∠ABF=∠FBC
在△EAB和△FBC中,
∴△EAB≌△FBC(SAS)
∴CF=AE 6分
∵AE=2BE
∴CF=2BE 7分
∴CE=CF+EF=3BE
(3)有(2)证明可知CF=AE, 9分
∵AE=mBE
∴CF=mBE 10分
∴CE=CF+EF=(m+1)BE 11分
∴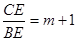 12分
12分
考点:1.三角形全等 2.等边三角形的性质. 3.线段的倍分关系.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com