
 ,AD=8,∠BMC=90°.①求线段AM的长;②若点N在边BC上,且∠AND=90°,则线段MN的长是______.
,AD=8,∠BMC=90°.①求线段AM的长;②若点N在边BC上,且∠AND=90°,则线段MN的长是______.
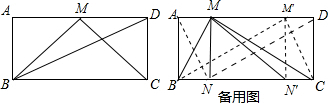
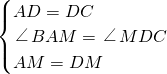 ,
,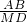 =
=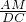 ,
, ,AD=8,
,AD=8, ,
,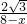 =
=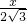 ,
, ,
,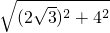 =2
=2 ,
, 或2
或2 .
.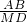 =
=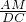 ,设AM=x,则DM=8-x,则
,设AM=x,则DM=8-x,则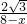 =
=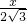 ,解得x1=2,x2=6,
,解得x1=2,x2=6, ;当AM=2,AN′=6(即N落在N′的位置),利用勾股定理可计算出MN′=2
;当AM=2,AN′=6(即N落在N′的位置),利用勾股定理可计算出MN′=2 ,所以MN的长为2
,所以MN的长为2 或2
或2 .
.

科目:初中数学 来源: 题型:
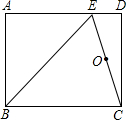 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.查看答案和解析>>
科目:初中数学 来源: 题型:
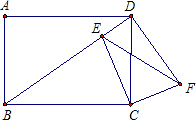 如图,在矩形ABCD中,点E对角线是BD上一点,作∠CEF=∠CBD,过点C作CF⊥CE交EF于F,连接DF.求证:
如图,在矩形ABCD中,点E对角线是BD上一点,作∠CEF=∠CBD,过点C作CF⊥CE交EF于F,连接DF.求证:| CE |
| CB |
| CF |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.
(2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:
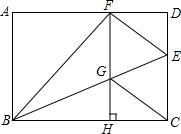 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com