
清朝康熙皇帝是我国历史上一位对数学很有兴趣的帝王,近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:
“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数.”
用现在数学语言表达是:
“若直角三角形的三边长分别为3、4,5的整数倍,设其面积为S,则
第一步: ;
;
第二步: ;
;
第三步:分别用3,4、5乘k,得三边长.”
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
科目:初中数学 来源: 题型:
| S |
| 6 |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
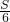 =m;第二步:
=m;第二步: =k;第三步:分别用3、4、5乘k,得三边长”.
=k;第三步:分别用3、4、5乘k,得三边长”.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
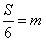 ;第二步:
;第二步: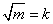 ;第三步:分别用3、4、5乘以k,得三边长。”
;第三步:分别用3、4、5乘以k,得三边长。” 查看答案和解析>>
科目:初中数学 来源:西城区模拟 题型:解答题
| S |
| 6 |
| m |
查看答案和解析>>
科目:初中数学 来源:2003年北京市西城区抽样测试初三试卷(解析版) 题型:解答题
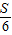 =m;第二步:
=m;第二步: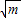 =k;第三步:分别用3、4、5乘k,得三边长”.
=k;第三步:分别用3、4、5乘k,得三边长”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com