
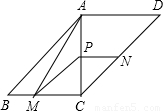
 ×BM×AC=
×BM×AC= ×x×2=x,
×x×2=x,


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源:2010年江苏省镇江市丹阳市吴塘中学九年级(下)数学阶段调研试卷(解析版) 题型:填空题
 CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .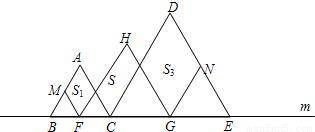
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《相交线与平行线》(03)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《相交线与平行线》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《图形认识初步》(02)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2010年江苏省徐州市树人中学中考数学二模试卷(解析版) 题型:填空题
 CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .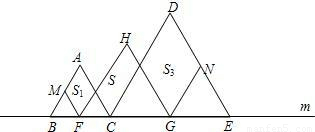
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com