Question

3、如图，∠BAC=∠ABD，请你添加一个条件：

∠C=∠D或AC=BD

，使OC=OD（只添一个即可）．

Answer 1

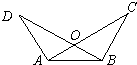
分析：本题可通过全等三角形来证简单的线段相等．△AOD和△BOC中，由于∠BAC=∠ABD，可得出OA=OB，又已知了∠AOD=∠BOC，因此只需添加一组对应角相等即可得出两三角形全等，进而的得出OC=OD．也可直接添加AC=BD，然后联立OA=OB，即可得出OC=OD．

解答：解：∵∠BAC=∠ABD，
∴OA=OB，又有∠AOD=∠BOC；
∴当∠C=∠D时，△AOD≌△BOC；
∴OC=OD．
故填∠C=∠D或AC=BD．

点评：本题考查了全等三角形的判定；题目是开放型题目，根据已知条件结合判定方法，找出所需条件，一般答案不唯一，只要符合要求即可．