
【题目】如图所示,再平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),![]() ,点C的坐标为(0,3).
,点C的坐标为(0,3).
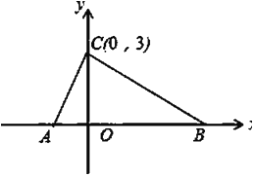
(1)求a,b的值;
(2)求![]() ;
;
(3)若点M在坐标轴上,且![]() =
=![]()
![]() ,直接写出M的坐标;
,直接写出M的坐标;
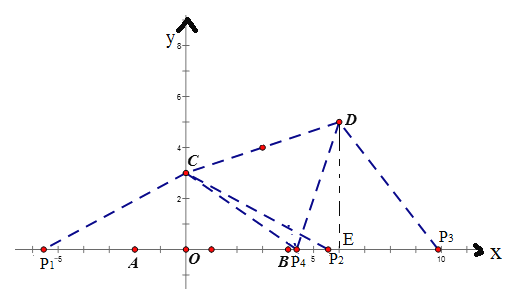
(4)点D的坐标为(6,5),动点P在x轴上,当△CDP试等腰三角形,请直接写出所有符合条件的点P的坐标.
【答案】(1)a=-2,b=4;(2)9;(3)(0,0)或(-4,0);(4)P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0),P4(
,0),P4(![]() ,0).
,0).
【解析】
(1)根据绝对值和算术平方根的非负性,求出a、b的值,求得A、B的坐标;
(2)根据三角形的面积公式求解;
(3)当M在![]() 轴上时,设点M的坐标为(x,0),根据AM的距离和三角形的面积S△ACM=
轴上时,设点M的坐标为(x,0),根据AM的距离和三角形的面积S△ACM=![]() S△ABC可求出AM的值,从而得到M的坐标;当M在
S△ABC可求出AM的值,从而得到M的坐标;当M在![]() 轴上时,设点M的坐标为
轴上时,设点M的坐标为![]() ,则
,则![]() 以
以![]() 为底,以
为底,以![]() 为高,根据S△ACM=
为高,根据S△ACM=![]() S△ABC可求出
S△ABC可求出![]() 的值,即可得到M的坐标.
的值,即可得到M的坐标.
(4)通过作图,可得: 当以∠C为顶角时,对应P1,P2;当以∠D为顶角时,对应P3;当以CD为底时,对应P4;根据勾股定理求解.
解:(1)∵|a+2|+![]() =0,∴a+2=0,b-4=0.
=0,∴a+2=0,b-4=0.
∴a=-2,b=4.
(2)由(1)得;点A(-2,0),点B(4,0).
又∵点C(0,3),
∴AB=|-2-4|=6,CO=3.
∴S三角形ABC=![]() AB·CO=
AB·CO=![]() ×6×3=9.
×6×3=9.
(3) 当M在![]() 轴上时,设点M的坐标为(x,0),
轴上时,设点M的坐标为(x,0),
则AM=|x-(-2)|=|x+2|.
又∵S△ACM=![]() S△ABC,
S△ABC,
∴![]() AM·OC=
AM·OC=![]() ×9,
×9,
∴![]() |x+2|×3=3.
|x+2|×3=3.
∴|x+2|=2.即x+2=±2,
解得x=0或-4,
所以点M的坐标为(0,0)或(-4,0).
当M在![]() 轴上时,设点M的坐标为
轴上时,设点M的坐标为![]() ,
,
则![]() ,
,
∵S△ACM=![]() S△ABC
S△ABC
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() .
.
所以点M的坐标为![]() 或
或![]() .
.
综上,点M的坐标为![]() ,
,![]() 或
或![]() .
.
(4)如图,点P的位置有四种情况:
当以∠C为顶角时,对应P1,P2;
当以∠D为顶角时,对应P3;
当以CD为底时,对应P4;
由已知可得:CD=![]()
所以OP1=OP2=![]() , EP3=
, EP3=![]()
所以P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0)
,0)
设P4(x,0),则根据等腰三角形性质和勾股定理可得:
![]()
解得
![]()
所以P4(![]() ,0)
,0)
综合上述:P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0),P4(
,0),P4(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为![]() 的滑动变阻器及一电流表测电源电压,结果如图所示.
的滑动变阻器及一电流表测电源电压,结果如图所示.
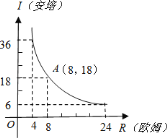
![]() 电流
电流![]() (安培)与电阻
(安培)与电阻![]() (欧姆)之间的函数解析式为________;
(欧姆)之间的函数解析式为________;
![]() 当电阻在
当电阻在![]() 之间时,电流应在________范围内,电流随电阻的增大而________;
之间时,电流应在________范围内,电流随电阻的增大而________;
![]() 若限制电流不超过
若限制电流不超过![]() 安培,则电阻在________之间.
安培,则电阻在________之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作图过程 .
已知:△![]() ,
,![]() .
.
求作:![]() 边上的高线.
边上的高线.
作法:如图,

①以点![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() 和点
和点![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点![]() ;
;
③作射线![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 就是所求作的
就是所求作的![]() 边上的高线.
边上的高线.
根据圆圆设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵![]() ,
,
∴点![]() 在线段
在线段![]() 的垂直平分线上(__________) (填推理的依据).
的垂直平分线上(__________) (填推理的依据).
∵__________=__________,
∴点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
∴![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.
∴![]() ⊥
⊥![]() .
.
∴线段![]() 就是
就是![]() 边上的高线.
边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,当
,….,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ;当
;当![]() 为大于1的偶数时,
为大于1的偶数时,![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)直接写出![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(3)计算:![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE交BC于点F,连接BE.
(1)求证:AB⊥BE;
(2)当AD=BF时,求∠BEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BE平分∠ABC,DE∥BC.

(1)试猜想△BDE的形状,并说明理由;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com