练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知是方程组  的解，则         ，=  　　　 ．


       

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


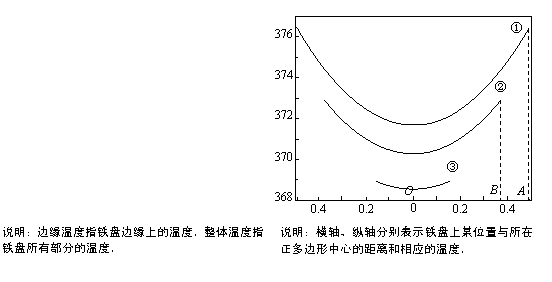
    在一次聚餐中，小明发现用圆形铁盘加热食物时，铁盘边缘部分的食物先熟，中间部分的食物后熟，说明铁盘不同位置的温度有差异．针对这一现象，他收集了如下统计图表：

    表一  正多边形铁盘温度方差表                 图一 正多边形铁盘温度分布统计图（部分）

     


    正多边形边数

    边缘温度方差

    整体温度方差

    4

    2.30

    4.73

    6

    0.34

    3.05

    8

    0.10

    2.60

    10

    0.05

    2.52

    12

    0.02

    2.51

    无穷多：圆

    0.00

    2.30

    （1）表一中，随着正多边形边数的增加，边缘温度方差如何变化？边缘温度最稳定的是哪一种形状的铁盘？

    （2）图一中，最有可能表示圆形铁盘温度分布的曲线序号是         ．

    （3）已知各正多边形（包含圆）的面积相等．图一中点A、B的数值对应曲线的端点，点O表示正多边形中心．观察图一，下列说法正确的有         ．（填写正确选项的序号）

    a．可以看出，曲线②表示的整体温度比曲线③表示的整体温度稳定．

    b．OA与OB长度不同，其意义是不同正多边形的顶点距各自中心的距离不同．

    c．曲线②表示的铁盘的边数比曲线①表示的铁盘的边数少．

    d．如果曲线①代表正四边形，且OA2︰OB2＝3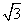︰4，那么曲线②可以代表正六边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在梯形ABCD中，AB∥CD，∠B＝90° ，连接AC，∠DAC＝∠BAC．若BC＝4cm，AD＝5cm，则梯形ABCD的周长为           cm．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是（   ）

    A.                                                 B.

    C.                                            D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    多项式的公因式是         .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：, 其中.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直角△ABC中，∠BAC =90°,D、E、F分别为AB、BC、AC的中点，已知DF=3，

    则AE=             .

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


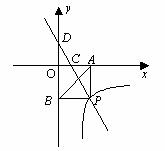
    如图，一次函数y＝kx＋3的图象分别交x轴、y轴于点C、点D，与反比例函数的图象在第四象限相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，－6）且S△DBP＝27.

    （1）求上述一次函数与反比例函数的表达式；

    （2）设点Q是一次函数y＝kx＋3图象上的一点，且满足△DOQ的面积是△COD面积的2倍，直接写出点Q的坐标.

    （3）若反比例函数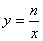的图象与△ABP总有公共点，直接写出n的取值范围.

    查看答案和解析>>

    同步练习册答案