
 根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.
根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.| 2 | x2-3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源:2015届江苏省盐城市七年级下学期期中考试数学试卷(解析版) 题型:解答题
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
(1)如图,一个边长为1的正方形,依次取正方形面积的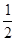 、
、 、
、
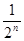 ,根据图示我们可以知道:
,根据图示我们可以知道: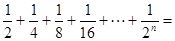 .
.

利用上述公式计算: .
.
(2)计算: ;
;
(3)计算: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.
根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题. .
.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
| 由多项式的乘法法则知:若(x+a)(x+b)=x2+x+q,则p=a+b,q=a·b;反过来x2+x+q=(x+a)(x+b)要将多项式x2+x+q进行分解,关键是找到两个数a、b,使a+b=p,a·b=q,如对多项式x2-3x+2,有p=-3,q=2,a=-1,b=-2。此时(-1)+(-2)=-3,(-1)(-2)=2,所以x2-3x+2可分解为(x-1)(x-2)即x2-3x-2=(x-1)(x-2)。 (1)根据以上填写下表: | ||||||||||||||||||||||||||||||
当q是正数时,应分解成两个因数a、b_______________号,a、b的符号与__________相同; 当q是负数时,应分解成的两个因数a、b______________号,a、b中绝对值较大的因数的符号与_______相同。 (3)分解因式: x2-x-12=_____________;x2-7x+6=________________。 |
查看答案和解析>>
科目:初中数学 来源:2010年广东省茂名市高州市“缅茄杯”学科竞赛试卷(初三数学)(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com