
【题目】出租车司机小王某天下午营运全是在南北走向的公路上进行的。如果向南记作“![]() ”,向北记作“
”,向北记作“![]() ”他这天下午行车情况如下:(单位:千米;每次行车都有乘客)
”他这天下午行车情况如下:(单位:千米;每次行车都有乘客)
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
请回答:
(![]() )小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
(![]() )若小王的出租车每千米耗油
)若小王的出租车每千米耗油![]() 升,不计汽车的损耗,共耗油多少升?
升,不计汽车的损耗,共耗油多少升?
(![]() )若规定每敞车的起步价是
)若规定每敞车的起步价是![]() 无,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收
无,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收![]() 元钱,那么小王这天下午收到乘客所给车费共多少元?
元钱,那么小王这天下午收到乘客所给车费共多少元?
【答案】(1)小王在下午出车的出发地的正南方向,距下午出车的出发地8千米;(2)9.6升;(3)104元.
【解析】
(1)根据题意计算行车情况的和进行判断即可;
(2)将行车情况的绝对值相加得到总路程,计算即可;
(3)先计算出总的起步价,然后加上超过3千米时额外收的费用.
解:(1)-2+4-1+10-3-2-4+6=8(千米),
答:小王在下午出车的出发地的正南方向,距下午出车的出发地8千米;
(2)|-2|+|4|+|-1|+|10|+|-3|+|-2|+|-4|+|6|=32(千米),0.3×32=9.6(升),
答:共耗油9.6升;
(3)10×8+2×(4-3)+ 2×(10-3)+ 2×(4-3)+ 2×(6-3)=104(元),
答:小王这天下午收到乘客所给车费共104元.


科目:初中数学 来源: 题型:
【题目】如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP![]() BE(点P、E在直线AB的同侧),如果
BE(点P、E在直线AB的同侧),如果![]() ,那么△PBC的面积与△ABC面积之比为【 】
,那么△PBC的面积与△ABC面积之比为【 】

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求证:AB⊥BD;
(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;
(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,△ABC, ∠ABC、∠ACB 的三等分线交于点 E、D, 若∠1=130°,∠2=110°,求∠A 的度数。
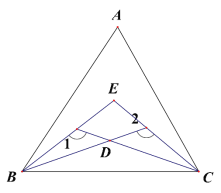
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E 若∠1=110°,∠2=130°,求∠A 的度数。
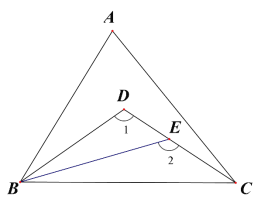
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是______(把正确说法的序号都填上)
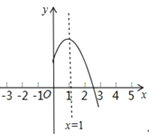
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,坐标原点O是菱形ABOC的一个顶点,边OB落在x轴的负半轴上,且cos∠BOC=![]() ,顶点C的坐标为(a,4),反比例函数
,顶点C的坐标为(a,4),反比例函数![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为平行四边形
为平行四边形![]() 的对角线,
的对角线,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 、
、![]() 相交于
相交于![]() ,直线
,直线![]() 交线段
交线段![]() 的延长线于
的延长线于![]() ,下面结论:①
,下面结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中正确的个数是( )
其中正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com