Question

19．教材中有如下一段文字：
思考
如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC，固定住长木棍，转动短木棍，得到△ABD，这个实验说明了什么？
如图中的△ABC与△ABD满足两边和其中一边的对角分别相等，即AB=AB，AC=AD，∠B=∠B，但△ABC与△ABD不全等．这说明，有两边和其中一边的对角分别相等的两个三角形不一定全等．
小明通过对上述问题的再思考，提出：两边分别相等且这两边中较大边所对的角相等的两个三角形全等．请你判断小明的说法正确．（填“正确”或“不正确”）

Answer 1

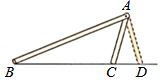
分析 小明的说法正确．如图，△ABC和△DEF中，AB＞AC，ED＞DF，AB=DE，AC=DF，∠ACB=∠DFE，作AG⊥BC于G，DH⊥EF于H．首先证明△ACG≌△DFH，推出AG=DH，再证明△ABG≌△DEH，推出∠B=∠E，由此即可证明△ABC≌△DEF．

解答 解：小明的说法正确．
理由：如图，△ABC和△DEF中，AB＞AC，ED＞DF，AB=DE，AC=DF，∠ACB=∠DFE，作AG⊥BC于G，DH⊥EF于H．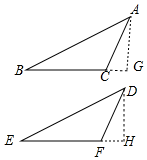

∵∠ACB=∠DFE，
∴∠ACG=∠DFH，
在△ACG和△DFH中，
$\left\{\begin{array}{l}{∠G=∠H}\\{∠ACG=∠DFH}\\{AC=DF}\end{array}\right.$，
∴△ACG≌△DFH，
∴AG=DH，
在Rt△ABG和Rt△DEH中，
$\left\{\begin{array}{l}{AB=DE}\\{AG=DH}\end{array}\right.$，
∴△ABG≌△DEH，
∴∠B=∠E，
在△ABC和△DEF中，
$\left\{\begin{array}{l}{∠B=∠E}\\{∠ACB=∠DFE}\\{AB=DE}\end{array}\right.$，
∴△ABC≌△DEF．
（当△ABC和△DEF是锐角三角形时，证明方法类似）．
故答案为正确．

点评 本题考查全等三角形的判定和性质等知识，解题的关键是理解题意，学会添加辅助线构造全等三角形解决问题，属于中考常考题型．