
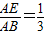 .点D在CB的延长线上,且ED=EC,求CD的长.
.点D在CB的延长线上,且ED=EC,求CD的长.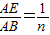 (n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.
(n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.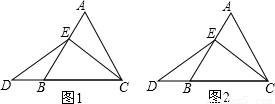
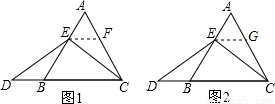 解:(1)∵EF∥BC,△ABC是等边三角形,
解:(1)∵EF∥BC,△ABC是等边三角形,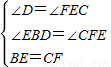 ,
, AB=
AB= ,
, =
=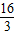 ;
;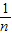 AB=
AB=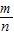 .
.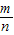 =
= .
.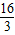 ;
;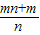 .
.

科目:初中数学 来源: 题型:
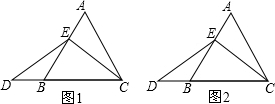 (2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.
(2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.| AE |
| AB |
| 1 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| AE |
| AB |
| 1 |
| n |
| mn+m |
| n |
| mn+m |
| n |
查看答案和解析>>
科目:初中数学 来源:广东省期中题 题型:单选题
查看答案和解析>>
科目:初中数学 来源:广东省期中题 题型:单选题
[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com