
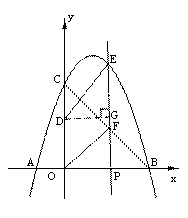
如图抛物线y=ax2+bx+3与x轴相交于点A(-1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式。(不必说明平分平行四边形面积的理由)
|
第26题图 |
备用图 |
备用图‚ |
解:(1)由抛物线经过点A(-1,0)、B(3,0)得,
![]() ………………………………………………………1分
………………………………………………………1分
解得,![]() ∴抛物线的解析式为
∴抛物线的解析式为![]() ; …………2分
; …………2分
(2)解法一: 设点P(m,0)
∵点P在抛物线![]() 上,
上,
 ∴PE=
∴PE=![]()
把![]() 代入
代入![]() 得,
得, ![]() ∴C(0,3) ……3分
∴C(0,3) ……3分
设直线BC解析式为![]() ,则
,则
![]()
解得![]() ∴直线BC解析式为
∴直线BC解析式为![]() …………4分 第26题 图①
…………4分 第26题 图①
∵点F在直线BC上,∴PF=![]()
∴EF=PE-PF=![]() ……………………………5分
……………………………5分
若四边形ODEF是平行四边形,则EF=OD=2
 ∴
∴![]() , ……………………………6分
, ……………………………6分
解得 ![]() ………………………………7分
………………………………7分
∴P(1,0)或 P(2,0) ………………………8分
解法二:如图②
把![]() 代入
代入![]() 得,
得, ![]() ∴C(0,3)
∴C(0,3)
设直线BC解析式为![]() ,则
,则
![]() 第26题 图②
第26题 图②
解得![]()
∴直线BC解析式为![]() …………3分
…………3分
过点D作DG⊥EF于点G,则四边形ODGP是矩形
∴DG=OP
若四边形ODEF是平行四边形 ∴DE∥OF
∴∠DEF=∠OFP
∵∠DGE=∠OPF=90°
∴△DEG≌△OFP
∴EG=FP ………………4分
设点P(m,0)∵点P在抛物线![]() 上,
上,
∴PE=![]() ………………5分
………………5分
∵点F在直线BC上,∴PF![]()
∵EG=![]() =
=![]()
∴![]() =
=![]() ……………………6分
……………………6分
∴![]() ,解得
,解得 ![]() ………7分
………7分
∴P(1,0)或 P(2,0) …………………8分
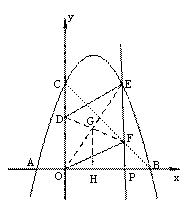 (3)当点P(2,0)时,即OP=2,如图③
(3)当点P(2,0)时,即OP=2,如图③
连接DF、OE相交于点G,取OP的中点H,连接GH
∵四边形ODEF是平行四边形
∴OG=GE
∴GH是△OEP的中位线
∴GH∥EP,GH=![]() PE
PE
把![]() =2代入
=2代入![]() 得,
得,![]() ,即PE=3
,即PE=3
∴GH=![]() 第26题图③
第26题图③
∵GH∥EP
∴GH⊥OP
∴G(1,![]() ) ……………………9分
) ……………………9分
设直线AG的解析式为![]() ,则
,则
 , ……………………10分
, ……………………10分
解得
∴将平行四边形ODEF的面积等分的直线解析式为![]() …11分
…11分
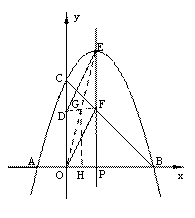
当点P(1,0)时,即OP=1,如图④
连接DF、OE相交于点G,取OP的中点H,连接GH,
 ∵四边形ODEF是平行四边形
∵四边形ODEF是平行四边形
∴OG=GE
∵OH=HP=![]() OP=
OP=![]()
∴GH是△OEP的中位线
∴GH∥EP,GH=![]() PE
PE
把![]() =1代入
=1代入![]() 得,
得,![]() ,即PE=4 第26题 ④图
,即PE=4 第26题 ④图
∴GH=2
∵GH∥EP ∴∠GHO=∠EPO=90°
∴G(![]() ,2) ……………………12分
,2) ……………………12分
设直线AG的解析式为![]() ,则
,则
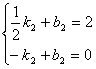 ……………………13分
……………………13分
解得
∴将平行四边形ODEF的面积等分的直线解析式为![]()
综上所述,直线解析式为 ![]() 或
或 ![]()


科目:初中数学 来源: 题型:
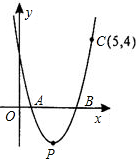 如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).查看答案和解析>>
科目:初中数学 来源: 题型:
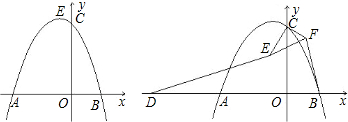
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com