
| 已知∠AOB=60°,半径为3cm的⊙P沿边OA从右向左平行移动,与边OA相切的切点记为点C。 |
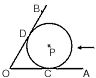 |
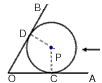
(1)⊙P移动到与边OB相切时(如图),切点为D,求劣弧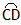 的长; 的长;(2)⊙P移动到与边OB相交于点E,F,若EF=4 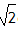 cm,求OC的长; cm,求OC的长; |
| 解:(1)连接PC,PD(如图1) ∵OA,OB与⊙P分别相切于点C,D, ∴∠PDO=∠PCO=90°, 又∵∠PDO+∠PCO+∠CPD+∠AOB=360°,∠AOB=60°, ∴∠CPD=120°, ∴ 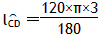 =2π; =2π;(2)可分两种情况: ①如图2,连接PE,PC,过点P作PM⊥EF于点M,延长CP交OB于点N ∵EF=4 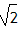 , ,∴EM=2 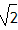 cm, cm,在Rt△EPM中,PM= 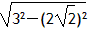 =1, =1,∵∠AOB=60°, ∴∠PNM=30°, ∴PN=2PM=2, ∴NC=PN+PC=5, 在Rt△OCN中,OC=NC·tan30°=5× 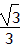 = =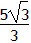 (cm); (cm);②如图3,连接PF,PC,PC交EF于点N,过点P作PM⊥EF于点M 由上一种情况可知,PN=2, ∴NC=PC-PN=1, 在Rt△OCN中,OC=NC·tan30°=1× 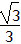 = =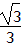 (cm), (cm),综上所述,OC的长为 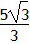 cm或 cm或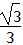 cm。 cm。 |
 | |图1 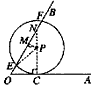 图2 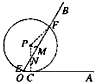 图3 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com