
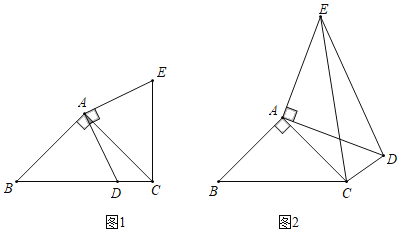
����Ŀ����ͼ1���ڡ�ABC�У���BAC��90����AB��AC��DΪBC����һ��(�����B��C�غ�)�����߶�AD�Ƶ�A��ʱ����ת90���õ�AE������EC.
(1)��ͼ1��ͨ��ͼ����ת�����ʿ�֪AD��_____����DAE��_____��.
��������⣩
(2)��ͼ1��֤��BC��DC+EC��
����չ���죩
��ͼ2���ڡ�ABC�У���BAC��90����AB��AC��DΪ��ABC��һ�㣬�ҡ�ADC��45�����Խ��߶�AD�Ƶ�A��ʱ����ת90���õ�AE������EC��ED.
(3)��AD��6��CD��3����BD�ij�.
���𰸡�(1)AE��90��(2)֤����������(3)BD=9.
��������
(1)������ת�任�����ʼ��ɽ�����⣻(2)֤����ABD�ա�ACE(SAS)���Ƴ�BD��CE���ɵý��ۣ�(3)��ͼ2�У���BD.֤����ABD�ա�ACE(SAS)���Ƴ�BD��CE����֤����ECD��ֱ�������Σ����ù��ɶ������ɽ������.
�⣺
(1)����ת�����ʿ�֪��AD��AE����DAE��90��.
�ʴ�ΪAE��90.
(2)��ͼ1�У�
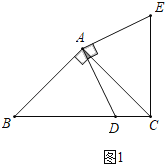
�ߡ�DAE����BAC��
���BAD����CAE��
�֡�AB��AC��AD��AE��
���ABD�ա�ACE(SAS)��
��BD��CE��
��BC��BD+DC��EC+CD.
(3)��ͼ2�У���BD.
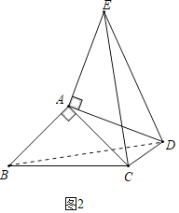
�ߡ�BAC����DAE��
��BAD����CAE��
�֡�AB��AC��AD��AE��
���ABD�ա�ACE(SAS)��
��BD��CE��
����ADE����ADC��45����
���ECDΪֱ�������Σ�
��EC2��CD2+ED2��CD2+2AD2��81��
��EC��9������BD�ij�Ϊ9.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y��x2��4��ͼ����x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ��CΪ���㣮һ�κ���y��mx+2��ͼ����A����y�ύ�ڵ�D��
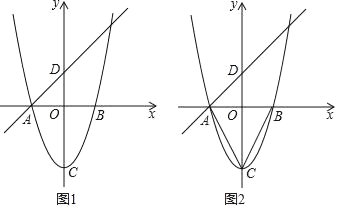
��1����ֱ��AD�ĺ�������ʽ��
��2��ƽ�Ƹ������ߵõ�һ���������ߣ����������ߵĶ���ΪC�������������ߵĶ����ԭ�����ߵĶ��������CC��ƽ����ֱ��AD���ҵ�1��x��3ʱ���������߶�Ӧ�ĺ���ֵ����СֵΪ��1�����������߶�Ӧ�ĺ�������ʽ��
��3����ͼ������AC��BC��������ƽ���ڣ�ֱ��д��ʹ����ACD����EBC���ƣ����е�A���E�Ƕ�Ӧ�㣩�ĵ�E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����۵�ij����Ʒÿ���ı����![]() Ԫ��������۵İ������ۣ��Կ�ӯ��
Ԫ��������۵İ������ۣ��Կ�ӯ��![]() ����ʱ������Ʒÿ���ڿ�����
����ʱ������Ʒÿ���ڿ�����![]() �����г����鷢�֣��ڰ������۵Ļ����ϣ�������Ʒÿ����
�����г����鷢�֣��ڰ������۵Ļ����ϣ�������Ʒÿ����![]() Ԫ��ÿ���ڿɶ���
Ԫ��ÿ���ڿɶ���![]() ������ÿ����Ʒ����
������ÿ����Ʒ����![]() Ԫ��
Ԫ��![]() Ϊ��������ÿ���ڵ�����Ϊ
Ϊ��������ÿ���ڵ�����Ϊ![]() Ԫ
Ԫ
��1���������Ʒÿ���Ľ���Ϊ����Ԫ��
��2�����ۼ�Ϊ����ʱ��ÿ���ڵ����������������Ƕ��٣�
��3��2019��2�¸�����Ʒÿ���ڵ��ۼ۾�Ϊÿ��![]() Ԫ����2019��2�µ�������
Ԫ����2019��2�µ�������![]() Ԫ�������
Ԫ�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������C1��y��a��x+2��2��5�Ķ���ΪP����x�������A��B���㣨��A�ڵ�B����ࣩ���ҵ�B������Ϊ��1��0��
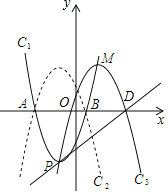
��1����������C1�ĺ�������ʽ��
��2����ͼ��������C2��������C1����x��Գƣ���������C2����ƽ�ƣ�ƽ�ƺ��������ΪC3��������C3�Ķ���ΪM������P��M���ڵ�O�����ĶԳ�ʱ�������M�����ꣻ����������C3�Ľ���ʽ��
��3���ڣ�2���������£���������C3��x��������ύ�ڵ�D����ֱ��PD���Ϸ���������C3�ϣ��Ƿ���ڵ�Qʹ����PDQ�������������ڣ��������Q�ĺ�����Ϊ��ֵʱ��PDQ����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��2mʱ��ˮ���4m��ˮ���½�2m��ˮ���������______m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
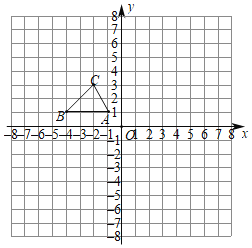
��1������![]() ���ڵ�O�����ĶԳƵ�
���ڵ�O�����ĶԳƵ�![]() ��
��
��2���Ե�AΪλ�����ģ���![]() �Ŵ�Ϊԭ����2�����õ�
�Ŵ�Ϊԭ����2�����õ�![]() �����ڵڶ������ڻ���
�����ڵڶ������ڻ���![]() ��
��
��3��ֱ��д���Ե�![]() ��
��![]() ��
��![]() Ϊ���㣬��
Ϊ���㣬��![]() Ϊһ�ߵ�ƽ���ı��εĵ��ĸ�����D�����꣮
Ϊһ�ߵ�ƽ���ı��εĵ��ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
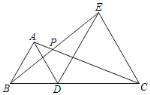
����Ŀ����ͼ��BC��8![]() cm����D���߶�BC�ϵ�һ�㣬�ֱ���BD��CDΪ����BC��ͬ�����ȱ�������ABD�͵ȱ�������CDE��AC��BE�ཻ�ڵ�P�����D�ӵ�B�˶�����Cʱ����P���˶�·�����������B��C�غϣ�Ϊ_____��
cm����D���߶�BC�ϵ�һ�㣬�ֱ���BD��CDΪ����BC��ͬ�����ȱ�������ABD�͵ȱ�������CDE��AC��BE�ཻ�ڵ�P�����D�ӵ�B�˶�����Cʱ����P���˶�·�����������B��C�غϣ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ����
����![]() �ķ�����������
�ķ�����������
��1����![]() ��ֵ��
��ֵ��
��2������ͼ������Щ���ޣ���ÿ�������ڣ�![]() ��
��![]() ������������仯��
������������仯��
��3����![]() ʱ����
ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������9�֣���ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() .����
.����![]() ��
��![]() �����ߣ���
�����ߣ���![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() .�벹ȫͼ�β������������⣺
.�벹ȫͼ�β������������⣺
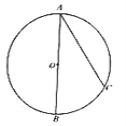
��1����֤��![]() ��
��
��2�����![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com