
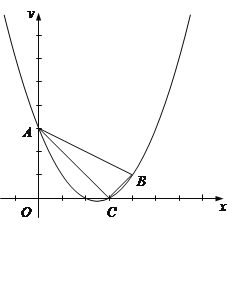
【题目】已知抛物线经过点![]() 、
、![]() 、
、![]() .
.
(1)求抛物线的解析式;
(2)联结AC、BC、AB,求![]() 的正切值;
的正切值;
(3)点P是该抛物线上一点,且在第一象限内,过点P作![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 在点
在点![]() 的上方,且
的上方,且![]() 与
与![]() 相似时,求点P的坐标.
相似时,求点P的坐标.
【答案】(1)![]() (2)
(2)![]() (3)点
(3)点![]() 的坐标为
的坐标为![]()
【解析】分析:(1)把A、B、C三点坐标带入抛物线解析式,利用待定系数法求解即可;
(2)由两点间的距离公式求得∴![]() 的长,由勾股定理的逆定理可判断
的长,由勾股定理的逆定理可判断![]() ,即可求得
,即可求得![]() 的值;
的值;
(3)当△APG与△ABC相似时,存在两种可能:∠PAG=∠CAB 和![]() ,分类讨论即可.
,分类讨论即可.
详解:(1)设所求二次函数的解析式为![]() ,
,
将![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )代入,得
)代入,得 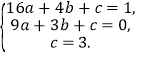
解得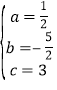 ,
,
所以,这个二次函数的解析式为![]() ;
;
(2)∵![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ,
,
∴![]() ;
;
(3)过点P作![]() ,垂足为H,
,垂足为H,
设![]()
![]() ,则
,则![]()
![]()
∵![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]()
∵![]()
∴当△APG与△ABC相似时,存在以下两种可能:
1° ∠PAG=∠CAB 则![]()
即![]() ∴
∴![]() 解得
解得![]() ;
;
∴点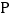 的坐标为
的坐标为![]() ;
;
2° ![]() ,则
,则![]()
即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]()


科目:初中数学 来源: 题型:
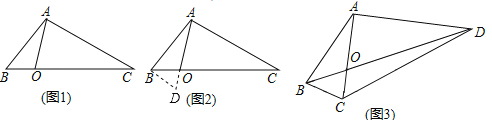
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图
就可以解决问题(如图![]() .
.
请回答:![]()
![]() ,
,![]() .
.
(2)请参考以上解决思路,解决问题:
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
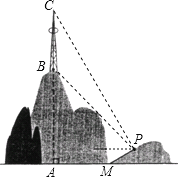
【题目】如图,山顶建有一座铁塔,塔高![]() 米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为
米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为![]() ,塔顶C点的仰角为
,塔顶C点的仰角为![]() 已测得小山坡的坡角为
已测得小山坡的坡角为![]() ,坡长
,坡长![]() 米
米![]() 求山的高度
求山的高度![]() 精确到1米
精确到1米![]() 参考数据:
参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
已知A、B两地相距48千米,甲骑自行车每小时走18千米,乙步行每小时走6千米,甲乙两人分别A、B两地同时出发.
(1)同向而行,开始时乙在前,经过多少小时甲追上乙?
(2)相向而行,经过多少小时两人相距40千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,若AB=4cm,AF=5cm,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为![]() 秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求
秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求![]() 的值;
的值;
②若点P、Q的运动路程分别为![]() (单位:cm,
(单位:cm,![]() ),已知A、C、P、Q四点为顶点的四边形是平行四边形,求
),已知A、C、P、Q四点为顶点的四边形是平行四边形,求![]() 与
与![]() 满足的数量关系式。
满足的数量关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+5x﹣2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若两个实数根分别为x1和x2,且x12+x22=23,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com