
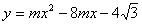 与
与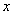 轴正半轴交于
轴正半轴交于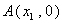 、
、 两点,且
两点,且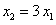 。
。
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
| 3 | 2 |
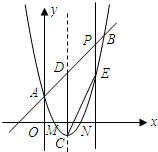 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江绍兴树人中学九年级第一学期期中学业评价数学试卷(解析版) 题型:解答题
如图,抛物线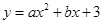 与
与 轴相交于点
轴相交于点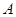 (﹣1,0)、
(﹣1,0)、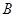 (3,0),与
(3,0),与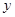 轴相交于点
轴相交于点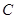 ,点
,点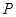 为线段
为线段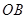 上的动点(不与
上的动点(不与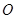 、
、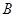 重合),过点
重合),过点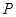 垂直于
垂直于 轴的直线与抛物线及线段
轴的直线与抛物线及线段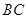 分别交于点
分别交于点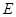 、
、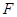 ,点
,点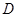 在
在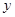 轴正半轴上,
轴正半轴上,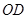 =2,连接
=2,连接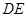 、
、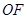 .
.
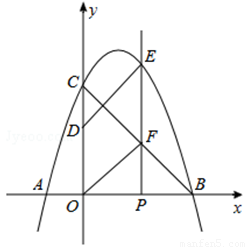
(1)求抛物线的解析式;
(2)当四边形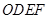 是平行四边形时,求点
是平行四边形时,求点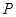 的坐标;
的坐标;
(3)过点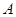 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形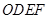 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() (
(![]() 为正整数)依次是直线
为正整数)依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() (
(![]() 为正整数),设
为正整数),设![]()
(1)求![]() 的值;
的值;
(2)求经过点![]() 的抛物线的解析式(用含
的抛物线的解析式(用含![]() 的代数式表示)
的代数式表示)
(3)定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
探究:当![]() 的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的
的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的![]() 的值.
的值.
 |
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
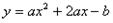 与
与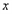 轴交于
轴交于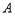 、
、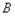 两点,与
两点,与 轴正半轴交于
轴正半轴交于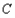 点,且
点,且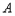 (
(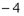 ,0),
,0),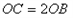
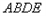 ,使
,使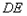 过点
过点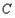 ,点
,点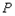 是
是 边上的一动点,连接
边上的一动点,连接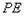 ,作
,作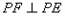 交
交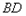 于点
于点 ,设线段
,设线段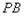 的长为
的长为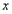 ,线段
,线段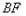 的长为
的长为 ,当
,当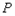 点运动时,求
点运动时,求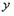 与
与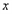 的函数关系式并写出自变量
的函数关系式并写出自变量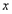 的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中
的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中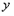 ≥0的部分有何关系?
≥0的部分有何关系?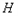 为其顶点,
为其顶点,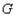 为抛物线上一动点(不与
为抛物线上一动点(不与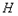 重合),取点
重合),取点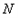 (
(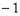 ,0),作
,0),作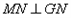 且
且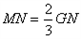 (点
(点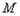 、
、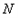 、
、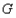 按逆时针顺序),当点
按逆时针顺序),当点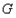 在抛物线上运动时,直线
在抛物线上运动时,直线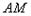 、
、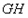 是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com