
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.

(1)判断DE与⊙O的位置关系并说明理由;
(2)求证: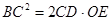
(3)若tanC=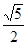 ,DE=2,求AD的长.
,DE=2,求AD的长.
(1)证明∠EDO=∠EBO=90°,所以DE与⊙O相切 (2)通过证明AC="2OE" ,BC2=CD·AC得BC2=2CD·OE
(3)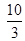
【解析】
试题分析:(1) DE与⊙O相切
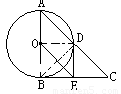
理由如下:连接OD,BD,
∵AB是直径,∴∠ADB=∠BDC=90°
∵E是BC的中点,∴DE=BE=CE,∴∠EDB=∠EBD,
∵OD=OB,∴∠OBD=∠ODB.
∴∠EDO=∠EBO=90°
∴DE与⊙O相切
(2)证明:由题意得OE是的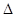 ABC的中位线,∴AC=2OE
ABC的中位线,∴AC=2OE
∵∠ABC=∠BDC=900,∠C=∠C ,∴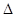 ABC∽
ABC∽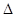 BDC
BDC
∴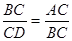 ,∴BC2=CD·AC,∴BC2=2CD·OE
,∴BC2=CD·AC,∴BC2=2CD·OE
(3) ∵DE=2
BC=4 AB=4. tanC
tanA=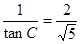 , 设BD=AD
, 设BD=AD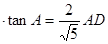 ,
,
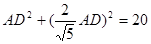
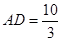
考点:直线与圆相切,相似三角形,三角函数
点评:本题考查直线与圆相切,相似三角形,三角函数,要求学生掌握直线与圆相切,会证明直线与圆相切,熟悉相似三角形的判定方法,会证明两个三角形相似


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com