Question

把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）。
（1）如图1，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子。

①要使折成的长方形盒子的底面积为484cm²，那么剪掉的正方形的边长为多少？
②折成的长方形盒子的侧面积是否有最大值？如果有，求出这个最大值及此时剪掉的正方形的边长；如果没有，请说明理由。
（2）如图2在正方形硬纸板上剪掉一些矩形（图2中阴影为剪去部分），将剩余部分折成一个有盖的长方形盒子，若折成的一个长方形盒子的表面积为550cm²，求此时长方形盒子的长、宽、高。

Answer 1

（1）①剪掉的正方形的边长为9cm。②长方形盒子的侧面积最大为800cm²。（2）剪掉的正方形的边长为15cm。此时长方体盒子的长为15cm，宽为10cm，高为5cm。

解析试题分析：解：（1）①设剪掉的正方形的边长为xcm。

则，即，
解得（不合题意，舍去），
，∴剪掉的正方形的边长为9cm。
②侧面积有最大值。设剪掉的正方形的边长为xcm，
盒子的侧面积为ycm²，则y与x的函数关系为：
，
即 ，即，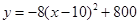
∴x=10时，y_最大=800。
即当剪掉的正方形的边长为10cm时，长方形盒子的侧面积最大为800cm²。
（2）设剪掉的正方形的边长为xcm。

解得：（不合题意，舍去），。
∴剪掉的正方形的边长为15cm。此时长方体盒子的长为15cm，宽为10cm，高为5cm。
考点：一元二次方程实际应用
点评：本题难度中等，主要考查学生对一元二次方程解决实际问题知识点的掌握，为中考常考题型，要求学生牢固掌握，注意培养数形结合思想，结合图像分析题意列方程。