Question

已知反比例函数的图象，当x取1，2，3，…，n时，对应在反比例图象上的点分别为M₁，M₂，M₃…，M_n，则=　　．

 

Answer 1

【答案】

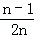
【解析】

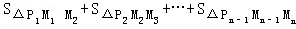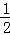试题分析：延长M_nP_n﹣1交M₁P₁于N，先根据反比例函数上点的坐标特点易求得M₁的坐标为（1，1）；Mn的坐标为（n，）；然后根据三角形的面积公式得=P₁M₁×P₁M₂+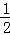M₂P₂×P₂M₃+…+M_n﹣1P_n﹣1×P_n﹣1M_n，而P₁M₂=P₂M₃=…=P_n﹣1M_n=1，则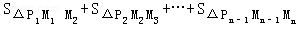=（M₁P₁+M₂P₂+…+M_n﹣1P_n﹣1），经过平移得到面积的和为M₁N，于是面积和等于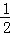（1﹣），然后通分即可．

解：延长M_nP_n﹣1交M₁P₁于N，如图，

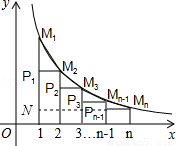
∵当x=1时，y=1，

∴M₁的坐标为（1，1）；

∵当x=n时，y=，

∴Mn的坐标为（n，）；

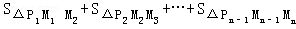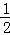∴=P₁M₁×P₁M₂+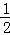M₂P₂×P₂M₃+…+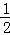M_n﹣1P_n﹣1×P_n﹣1M_n=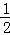（M₁P₁+M₂P₂+…+M_n﹣1P_n﹣1）

=M₁N

=（1﹣）

=．

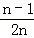故答案为．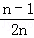

考点：反比例函数综合题．

点评：本题考查了反比例函数综合题：点在反比例函数图象上，点的横纵坐标满足反比例函数的解析式；掌握三角形的面积公式．