
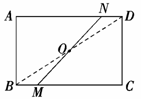
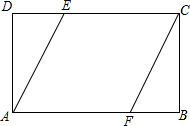
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
(1)求证:BM=DN;
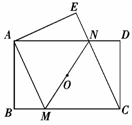
(2)如图②,四边形AMNE是由四边形CMND沿MN翻折得到的,连接CN,求证:四边形AMCN是菱形;
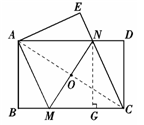
(3)在(2)的条件下,若△CDN的面积与△CMN的面积比为13,求![]() 的值.
的值.
 |
(1)证法一:连接BD,则BD过点O.
∵AD∥BC, ∴∠OBM=∠ODN.
又OB=OD, ∠BOM=∠DON,
∴△OBM≌△ODN.
∴BM=DN.
证法二:∵矩形ABCD是中心对称图形,点O是对称中心.
∴B、D和M、N关于O点中心对称.
∴BM=DN.
(2)证法一:∵矩形ABCD,
∴AD∥BC,AD=BC.
又BM=DN, ∴AN=CM.
∴四边形AMCN是平行四边形.
由翻折得,AM=CM,
∴四边形AMCN是菱形.
证法二:由翻折得,AN=NC,AM=MC,
∠AMN=∠CMN.
∵AD∥BC, ∴∠ANM=∠CMN.
∴∠AMN=∠ANM. ∴AM=AN.
∴AM=MC=CN=NA.
∴四边形AMCN是菱形.
(3)解法一:∵![]() ,
,![]() ,
,
又![]() :
:![]() =13,
=13,
∴DNCM=13
设DN=k,则CN=CM=3k.
过N作NG⊥MC于点G,
则CG=DN=k,MG=CM-CG=2k.
NG=![]()
∴MN=![]()
∴ ![]() .
.
解
法二:∵![]() ,
,![]() ,
,
又![]() :
:![]() =13, ∴DNCM=13
=13, ∴DNCM=13
连接AC,则AC过点O,且AC⊥MN.
设DN=k,则CN=AN=CM=3k,AD=4 k.
CD=![]()
OC=![]()
∴MN=![]()
∴ ![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,tan∠DAE=
,tan∠DAE=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知在矩形ABCD中.
已知在矩形ABCD中.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.
已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com