����⣺��1����������κ����Ľ���ʽΪ
y=a��x+1����x-2������1�֣�
�ѵ�C��0��2������������У����a=-1��
y=-��x+1����x-2��=-x
2+x+2=-��x-
��
2+
��������κ����Ľ���ʽΪ��
y=-x
2+x+2��3�֣�
����M������ΪM��
��
������4�֣�
[Ҳ����Ϊһ��ʽy=ax
2+bx+c����A��B��C�������������]
��2�����߶�BM����ֱ�ߵĽ���ʽΪ��y=kx+b����5�֣�
�ֱ��B��2��0����M��
��
�������������
���k=-
��b=3��
��y=-
x+3��
��N��������x��t�������t=-
x+3��
���x=2-
t����6�֣�
��ͼ�ο�֪��s=S
��AOC+S
����OQNC��7�֣�
=
��1��2+
��2+t����2-
t��
����������s=-
t
2+
t+3����8�֣�
����0��t��
����9�֣�
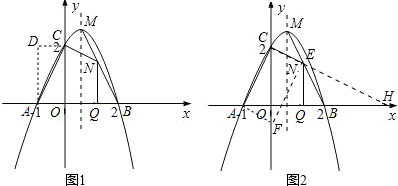
��3���Ե�O����A�����O����C��Ϊ���ε��������㣬
�������������ھ�����һ��OA�����OC���ĶԱ��ϣ�
����ͼ1����ʱ��δ֪���������ǵ�D��-1��2������10�֣�
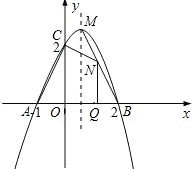
�Ե�A����CΪ���ε��������㣬���������㣨����O��
���ھ�����һ��AC�ĶԱ��ϣ�����ͼ2����ʱ
δ֪����ֱ�Ϊ��E����F����11�֣�
���ǵ�����������£�
��ACEF����
���ACEΪֱ�ǣ��ӳ�CE��x���ڵ�H��
����Rt��HOC��Rt��COA��
��
=�����OH=4��
���H������H��4��0����������߶�CH����ֱ�ߵ�
����ʽΪ��y=-
x+2����12�֣�
�߶�AC����ֱ�ߵ�
����ʽΪ��y=2x+2���߶�EF����ֱ�߹�ԭ������
�߶�AC����ֱ��ƽ�У��Ӷ��ɵ��߶�EF����ֱ�ߵ�
����ʽΪ��y=2x����13�֣�
�߶�AF����ֱ����ֱ��CHƽ�У�
��ֱ��AF�Ľ���ʽΪ��y=-
x+m��
��A��-1��0��������룬���m=-
��
��ֱ��AFΪ��y=-
x-
��
�ߵ�E��ֱ��CH��ֱ��EF�Ľ��㣻
��F��ֱ��AF��ֱ��EF�Ľ��㣬
����������������飺
��
��
���E��
��
����F��-
��-
������14�֣�
����ε�δ֪����Ϊ��-1��2����
��
������-
��-
����

 ��֪����A��B��C����Ķ��κ���ͼ����ͼ��ʾ��
��֪����A��B��C����Ķ��κ���ͼ����ͼ��ʾ��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
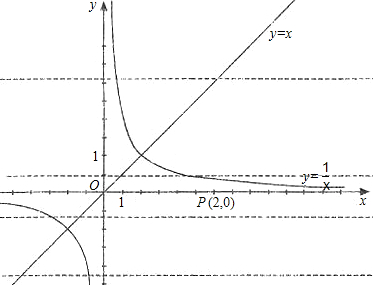
 ��ͼ����ƽ��ֱ������ϵxOy�У�AO=8��AB=AC��sin��ABC=
��ͼ����ƽ��ֱ������ϵxOy�У�AO=8��AB=AC��sin��ABC=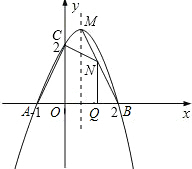 ��֪����A��B��C����Ķ��κ���ͼ����ͼ��ʾ��
��֪����A��B��C����Ķ��κ���ͼ����ͼ��ʾ��