
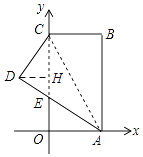
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为 . 
【答案】(﹣ ![]() ,
,![]() )
)
【解析】解:如图,过D作DH⊥y轴于H,
∵点B的坐标为(1,4),
∴AO=1,AB=4,
根据折叠可知:CD=BC=1,∠BAC=∠DAC,
由AB∥CO,可得∠BAC=∠OCA,
∴∠DAC=∠OCA,
∴CE=AE,
∴OE=DE,
设OE=x,则CE=4﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(4﹣x)2=x2+12,
∴x= ![]() ,
,
∴DE= ![]() ,CE=
,CE= ![]() ,
,
又∵DH⊥CE
∴ ![]() CE×DH=
CE×DH= ![]() CD×DE,
CD×DE,
∴DH= ![]() =
= ![]() ,
,
∴Rt△CDH中,CH= ![]() =
= ![]() ,
,
∴OH=4﹣ ![]() =
= ![]() ,
,
∵点D在第二象限,
∴D(﹣ ![]() ,
, ![]() ),
),
所以答案是:(﹣ ![]() ,
, ![]() ).
).
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() .求
.求![]() .以下是某位同学的解答过程,请在横线上填空,将解答过程补充完整.
.以下是某位同学的解答过程,请在横线上填空,将解答过程补充完整.

解:分别过![]() 的平行线
的平行线![]()
∵![]() (辅助线)
(辅助线)
∴![]() (如果两条直线都与第三条直线平行,那么这两条直线平行)
(如果两条直线都与第三条直线平行,那么这两条直线平行)
∴![]()
![]() ( )
( )
![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() (等式的性质)
(等式的性质)
∵![]() (已证)
(已证)
∴![]() (等式的性质)
(等式的性质)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (等量代换)
(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的各边分别平行于x轴或y轴,A,B,C,D的坐标分别为(﹣2,1)(2,1)(2,﹣1)(﹣2,﹣1)物体甲和物体乙分别由E(﹣2,0)和F(2,0)同时出发,沿长方形的边按逆时针方向同向行进,甲的速度每秒4个单位长度,乙的速度每秒1个单位长度,则两个物体第2019次相遇地点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
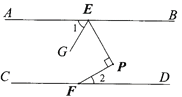
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如:![]() <0等。那么如何求出它们的解集呢?
<0等。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
若a>0,b>0,则![]() >0;若a<0,b<0,则
>0;若a<0,b<0,则![]() >0;
>0;
若a>0,b<0,则![]() <0;若a<0,b>0,则
<0;若a<0,b>0,则![]() <0.
<0.
反之:若![]() >0,则
>0,则![]() 或
或![]() ,
,
(1)若![]() <0,则___或___.
<0,则___或___.
(2)根据上述规律,求不等式![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
①画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
②画出△ABC向下平移3个单位的△AB2C2 , 并写出点C的对应点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E在BC上,AB=BE,BF平分∠ABC交AD于点F,请用无刻度的直尺画图(保留作图痕迹,不写画法).
(1)在图1中,过点A画出△ABF中BF边上的高AG;
(2)在图2中,过点C画出C到BF的垂线段CH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.
试根据统计图中提供的数据,回答下面问题:
(1)计算样本中,成绩为98分的学生有分,并补全条形统计图.
(2)样本中,测试成绩的中位数是分,众数是分.
(3)若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合速度测试将有多少名学生可以获得满分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com