
已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
1.求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
2.在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
3.如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.

1.过点 作
作 于点
于点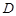 .(如图①)
.(如图①)
∵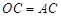 ,
, ,∴
,∴ .
.
∵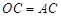 ,
, , ∴
, ∴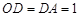 .
.
在Rt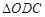 中,
中,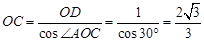
当 时,
时,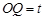 ,
, ,
, ;
;
过点 作
作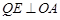 于点
于点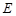 .(如图①)
.(如图①)

在Rt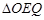 中,∵
中,∵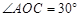 ,∴
,∴ ,
,
∴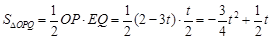 .
.
即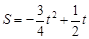 .………………………………………2分
.………………………………………2分
2.当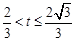 时,(如图②)
时,(如图②)
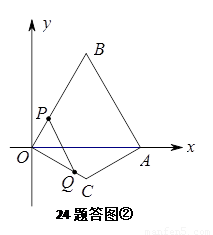
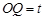 ,
,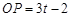 .
.
∵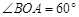 ,
,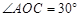 ,∴
,∴ .
.
∴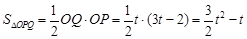 .
.
即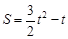 .
.
故当 时,
时,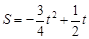 ,当
,当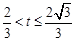 时,
时,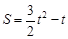 ……………4分
……………4分
 或
或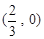 …………………6分
…………………6分
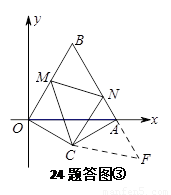
3. 的周长不发生变化.
的周长不发生变化.
延长 至点
至点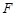 ,使
,使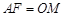 ,连结
,连结 .(如图③)
.(如图③)
∵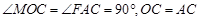 ,∴
,∴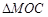 ≌
≌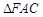 .
.
∴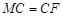 ,
,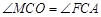 …………………7分
…………………7分
∴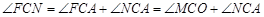
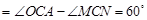 .
.
∴ . 又∵
. 又∵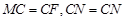 .
.
∴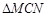 ≌
≌ .∴
.∴ ……………………………………9分
……………………………………9分
∴


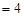 .
.
∴ 的周长不变,其周长为4 ……………………………………10分
的周长不变,其周长为4 ……………………………………10分
【解析】(1)由于点Q从点O运动到点C需要 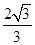 秒,点P从点A→O→B需要
秒,点P从点A→O→B需要 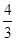 秒,所以分两种情况讨论:①0<t<
秒,所以分两种情况讨论:①0<t< ;②
;②
 ≤t<
≤t<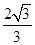 .针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围
.针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围
(2)如果△OCD为等腰三角形,那么分D在OA边或者OB边上两种情形.每一种情形,都有可能O为顶点,C为顶点,D为顶点,分别讨论,得出结果;
(3)如果延长BA至点F,使AF=OM,连接CF,则由SAS可证△MOC≌△FAC,得出MC=CF,再由SAS证出△MCN≌△FCN,得出MN=NF,那么△BMN的周长=BA+BO=4.


科目:初中数学 来源: 题型:
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
2
| ||
| 3 |
| 3 |
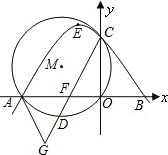 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧 |
| OA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com