
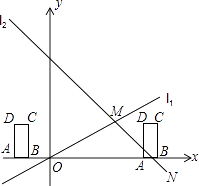
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��l1��y= ![]() x��ֱ��l2��y=��x+6�ཻ�ڵ�M��ֱ��l2��x���ཻ�ڵ�N��
x��ֱ��l2��y=��x+6�ཻ�ڵ�M��ֱ��l2��x���ཻ�ڵ�N��
��1����M��N�����꣮
��2������ABCD�У���֪AB=1��BC=2����AB��x���ϣ�����ABCD��x������������ÿ��1����λ���ȵ��ٶ��ƶ��������ABCD���OMN���ص����ֵ����ΪS���ƶ���ʱ��Ϊt���ӵ�B���O�غ�ʱ��ʼ��ʱ������A���N�غ�ʱ��ʱ��ʼ��������ֱ��д��S���Ա���t֮��ĺ�����ϵʽ������Ҫ���������̣���
��3���ڣ�2���������£���tΪ��ֵʱ��S��ֵ���������ֵ��
���𰸡�
��1��
�⣺�ⷽ����  ��
��
��ã� ![]() ��
��
��M�������ǣ���4��2����
�ڽ���ʽy=��x+6�У���y=0����ã�x=6����N�������ǣ���6��0��
��2��
�⣺��0��t��1ʱ���غϲ�����һ�������Σ�OB=t������� ![]() t���������
t��������� ![]() ��t
��t ![]() t=
t= ![]() t2��
t2��
��1��t��4ʱ���غϲ�����ֱ�����Σ����εĸ���1���µ��ǣ� ![]() t���ϵ��ǣ�
t���ϵ��ǣ� ![]() ��t��1�����������ε������ʽ���Եõ���S=
��t��1�����������ε������ʽ���Եõ���S= ![]() [
[ ![]() t+
t+ ![]() ��t��1��]=
��t��1��]= ![]() ��t��
��t�� ![]() ����
����
��4��t��5ʱ����M��x��Ĵ��ߣ����غϲ��ֱ����߷ֳ�����ֱ�����Σ��������ε��µ���2���ϵֱ��ǣ���t+6�� ![]() ��t��1�����������ε������ʽ�������
��t��1�����������ε������ʽ�������
S=�� ![]() t2+
t2+ ![]() t��
t�� ![]() ��
��
��5��t��6ʱ���غϲ�����ֱ�����Σ��뵱1��t��4ʱ���غϲ�����ֱ�����εļ��㷽����ͬ����S= ![]() ��13��2t����
��13��2t����
��6��t��7ʱ���غϲ�����ֱ�������Σ����뵱0��t��1ʱ���ⷨ��ͬ���������S= ![]() ��7��t��2��
��7��t��2��
��S= 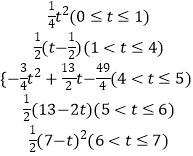
��3��
�⣺��0��t��1ʱ������ֵy��t�������������t=1ʱ��ȡ�����ֵ�ǣ� ![]() ��
��
��1��t��4ʱ������ֵy��t�������������t=4ʱ��ȡ�����ֵ�ǣ� ![]() ��4��
��4�� ![]() ��=
��= ![]() ��
��
��4��t��5ʱ���Ƕ��κ������Գ���t= ![]() �������ֵ�ǣ���
�������ֵ�ǣ��� ![]() ����
���� ![]() ��2+
��2+ ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��5��t��6ʱ������ֵy��t���������С�����Ժ���һ��С�� ![]() ��
��
ͬ������6��t��7ʱ��y��t���������С�����Ժ���һ��С�� ![]() ��
��
���Ժ��������ֵ�ǣ� ![]()
����������1��������ֱ�ߵĽ���ʽ��ɵķ�����Ľ⣬������ý���M�����꣬��y=��x+6�У���y=0������õ�N�ĺ����꣬��N�����꼴����⣻��2���ֳ�0��t��1��1��t��4��4��t��5��5��t��6��6��t��7������������������ε������ʽ�����ε������ʽ��������ú����Ľ���ʽ����3���ֱ����ÿ������º�������ֵ����ֵ�ķ�Χ������ȷ����
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����F�ڱ�AC�ϣ�����CF=2����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F������DF�����������ĸ����ۣ��١�AEF~��CAB����CF=2AF����DF=DC����tan��CAD= ![]() .������ȷ�Ľ����У� ��
.������ȷ�Ľ����У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˳������ܵ�̼�����ij��˾�Լ��������õ��շ������¹涨��һ������һ�����õ���������aǧ��ʱ����һ���µĵ��Ϊ20Ԫ��������aǧ��ʱ������˽�20Ԫ�⣬��������ÿǧ��ʱҪ�� ![]() Ԫ��ij����3�·��õ�80ǧ��ʱ�������35Ԫ��4�·��õ�45ǧ��ʱ�������20Ԫ��
Ԫ��ij����3�·��õ�80ǧ��ʱ�������35Ԫ��4�·��õ�45ǧ��ʱ�������20Ԫ��
��1����a��ֵ��
��2����������5�·ݽ����45Ԫ����ô�����ᵱ���õ���Ϊ����ǧ��ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪P���߶�AB�Ļƽ�ָ�㣬��PA��PB����S1��ʾPAΪһ�ߵ������ε������S2��ʾ����AB������PB�ľ��ε��������S1S2 �� ���������=�������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ�е���������P1��x1 �� y1����P2��x2 �� y2�������ǰ�|x1��x2|+|y1��y2|����P1��P2������ֱ�Ǿ��룬����d��P1 �� P2����
��1����֪OΪ����ԭ�㣬����P��x��y������d��O��P��=1����д��x��y֮������Ĺ�ϵʽ������������ֱ������ϵ�л������з��������ĵ�P����ɵ�ͼ�Σ�
��2����P0��x0 �� y0����һ���㣬Q��x��y����ֱ��y=ax+b�ϵĶ��㣬���ǰ�d��P0 �� Q������Сֵ����P0��ֱ��y=ax+b��ֱ�Ǿ��룮�����M��2��1����ֱ��y=x+2��ֱ�Ǿ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�з�����5����ͼ��ʾ�������Σ�����Ӱ��ʾ������B1��y���ϣ���C1��E1��E2��C2��E3��E4��C3��x���ϣ���������A1B1C1D1�ı߳�Ϊ1����B1C1O=60�㣬B1C1��B2C2��B3C3 �� ���A3��x��ľ����ǣ� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��������Ǻ������з��֣�����ͼ��ʾ�ľ���ֽƬABCD�ع���B��ֱ���۵���ʹ��A����BC�ϵĵ�E������ԭ�����ع���E��ֱ���۵���ʹ��A����BC�ϵĵ�F���������Ϳ������67.5��ǵ�����ֵ�ǣ� �� 
A.![]() +1
+1
B.![]() +1
+1
C.2.5
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com