
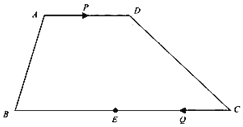
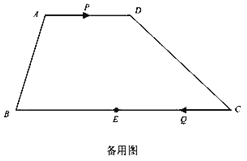
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从点
同时以每秒3个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.
也随之停止运动.
(1)当运动时间![]() 为多少秒时,
为多少秒时,![]() ;
;
(2)当运动时间![]() 为多少秒时,以点
为多少秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)![]() ,
,![]() ,求
,求![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系和自变量
的函数关系和自变量![]() 的取值范围.
的取值范围.
【答案】(1)当运动时间![]() 为1.5秒时,
为1.5秒时,![]() ;(2)当运动时间
;(2)当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;(3)
为顶点的四边形是平行四边形;(3)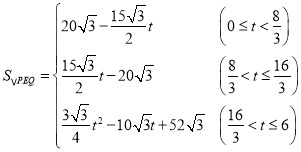
【解析】
(1)根据![]() 、
、![]() 可判定四边形
可判定四边形![]() 为平行四边形,此时
为平行四边形,此时![]() ,可得方程
,可得方程![]() ,解方程即可得解;
,解方程即可得解;
(2)分别从当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形和当
为平行四边形和当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形两方面分析求解即可求得答案;
为平行四边形两方面分析求解即可求得答案;
(3)分别从当![]() 在线段
在线段![]() 上时、当
上时、当![]() 与
与![]() 重合时、当
重合时、当![]() 在线段
在线段![]() 上时、当
上时、当![]() 在线段
在线段![]() 上时四方面进行讨论,从而确定
上时四方面进行讨论,从而确定![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系和自变量
的函数关系和自变量![]() 的取值范围.
的取值范围.
解:(1)如图示,
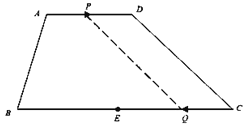
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
又∵![]() ,
,![]()
∴![]() .
.
当运动时间![]() 为1.5秒时,
为1.5秒时,![]() .
.
(2)由题意知,此时有两种情况,![]() 在
在![]() 上或
上或![]() 在
在![]() 上,
上,
①当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形
为平行四边形
此时![]() ,
,
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 满足题意
满足题意
②当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形
为平行四边形
此时![]() .
.
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 满足题意;
满足题意;
当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
(3)如图,过点![]() 作,
作,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]()
∴![]()
∴![]() .
.
∴![]()
①如图(1),
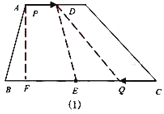
当![]() 在线段
在线段![]() 上时,
上时,![]() .
.
此时![]() ,
,![]() ,即:
,即:![]()
![]()
![]() .
.
②当![]() 与
与![]() 重合时,
重合时,![]() ,此时
,此时![]() 不存在;
不存在;
③当![]() 在线段
在线段![]() 上时,如图(2)
上时,如图(2)

![]()
此时![]() ,且
,且![]()
即:![]()
![]()
![]()
④当![]() 在线段
在线段![]() 上时,如图(3),联结
上时,如图(3),联结![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]()
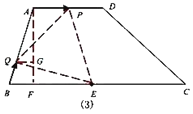
此时![]() ,且
,且![]() ,即:
,即:![]() .
.
![]() 梯形
梯形![]()
![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
∴![]()
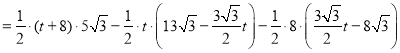
![]()
综上所述,![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系及自变量
的函数关系及自变量![]() 的取值范围为
的取值范围为
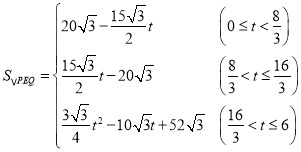
故答案是:(1)当运动时间![]() 为1.5秒时,
为1.5秒时,![]() ;(2)当运动时间
;(2)当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;(3)
为顶点的四边形是平行四边形;(3)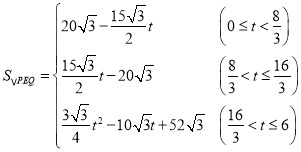 .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
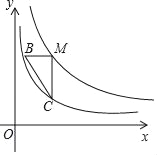
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
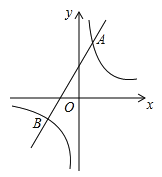
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
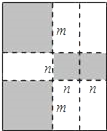
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]() ;
;
(2)已知x=![]() +3, y=
+3, y=![]() -3,求下列各式的值:①x2-2xy+y2;②x2-y2;
-3,求下列各式的值:①x2-2xy+y2;②x2-y2;
(3)已知a、b、c满足![]()
求:①a、b、c的值;
②请判断以a、b、c为边构成三角形的形状(按角分类),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红和小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元,且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)为了奖励更多的同学,学校决定再次购进甲、乙两种笔记本,若买甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购买这两种笔记本的总金额不超过320元,求这次购买乙种笔记本最多多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF、EC,且CF=EF,下列结论正确的个数是( )
①CF平分∠BCD;②∠EFC=2∠CFD;③∠ECD=90°;④CE⊥AB.
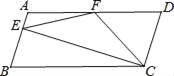
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com