
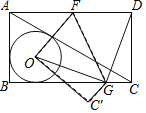
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
A.BC﹣AB=2B.AC=2ABC.AF=CDD.CD+DF=5
【答案】C
【解析】
如图,设⊙O与BC的切点为M,连接MO并延长MO交AD于点N,根据折叠的性质得到OG=DG,根据全等三角形的性质得到OM=GC=1,CD=GM=BC﹣BM﹣GC=BC﹣2即可判断A;设AB=a,BC=b,AC=c,⊙O的半径为r,推出⊙O是Rt△ABC的内切圆可得r=![]() (a+b﹣c),根据勾股定理得到BC+AB=2
(a+b﹣c),根据勾股定理得到BC+AB=2![]() +4,AC=
+4,AC=![]() =2(1+
=2(1+![]() ),即可判断B;再设DF=x,在Rt△ONF中,FN=3+
),即可判断B;再设DF=x,在Rt△ONF中,FN=3+![]() ﹣1﹣x,OF=x,ON=1+
﹣1﹣x,OF=x,ON=1+![]() ﹣1,由勾股定理可得x=4﹣
﹣1,由勾股定理可得x=4﹣![]() ,即可判断D和C.
,即可判断D和C.
解:如图,设⊙O与BC的切点为M,连接MO并延长MO交AD于点N,
∵将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,
∴OG=DG,
∵OG⊥DG,
∴∠MGO+∠DGC=90°,
∵∠MOG+∠MGO=90°,
∴∠MOG=∠DGC,
在△OMG和△GCD中,
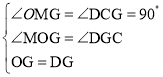 ,
,
∴△OMG≌△GCD,(AAS),
∴OM=GC=1,CD=GM=BC﹣BM﹣GC=BC﹣2.
∵AB=CD,
∴BC﹣AB=2.故A正确;
设AB=a,BC=b,AC=c,⊙O的半径为r,
⊙O是Rt△ABC的内切圆可得r=![]() (a+b﹣c),
(a+b﹣c),
∴c=a+b﹣2.
在Rt△ABC中,由勾股定理可得a2+b2=(a+b﹣2)2,
整理得2ab﹣4a﹣4b+4=0,
又∵BC﹣AB=2即b=2+a,代入可得2a(2+a)﹣4a﹣4(2+a)+4=0,
解得a1=1﹣![]() (舍去),a2=1+
(舍去),a2=1+![]() ,
,
∴BC+AB=2![]() +4,
+4,
∴AB=1+![]() ,BC=3+
,BC=3+![]() ,
,
∴AC=![]() =2(1+
=2(1+![]() ),
),
∴AC=2AB;故B正确;
再设DF=x,在Rt△ONF中,FN=3+![]() ﹣1﹣x=2+
﹣1﹣x=2+![]() ﹣x,OF=x,ON=1+
﹣x,OF=x,ON=1+![]() ﹣1=
﹣1=![]() ,
,
由勾股定理可得(2+![]() ﹣x)2+(
﹣x)2+(![]() )2=x2,
)2=x2,
解得x=4﹣![]() ,
,
∴CD﹣DF=![]() +1﹣(4﹣
+1﹣(4﹣![]() )=2
)=2![]() ﹣3,CD+DF=
﹣3,CD+DF=![]() +1+4﹣
+1+4﹣![]() =5,故D正确;
=5,故D正确;
∴AF=AD﹣DF=2![]() ﹣1,
﹣1,
∴AF≠CD,故C错误;
故选:C.


科目:初中数学 来源: 题型:
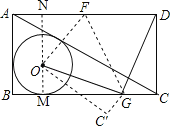
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD在直角坐标系中,其中AB边在y轴上,其余各边均与坐标轴平行,直线l:y=x﹣5沿y轴的正方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )

A.3![]() B.5
B.5![]() C.6
C.6![]() D.10
D.10![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
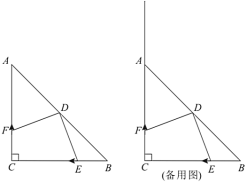
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
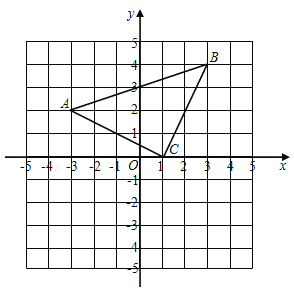
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为B(3,4)、A(﹣3,2)、C(1,0),正方形网格中,每个小正方形的边长是一个单位长度.
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格上画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,点C2的坐标是 ;(画出图形)
(3)若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com