
【题目】如图,抛物线![]() 过
过![]() ,
,![]() 两点.
两点.
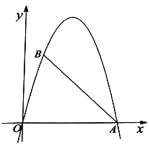
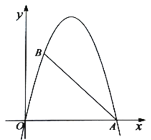
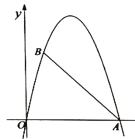
备用图1 备用图2
(1)求该抛物线的解析式;
(2)点![]() 是抛物线上一点,且位于第一象限,当
是抛物线上一点,且位于第一象限,当![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标;
的坐标;
(3)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?存在,求出点
两部分?存在,求出点![]() 的坐标;不存在,请说明理由.
的坐标;不存在,请说明理由.
【答案】(1)抛物线的表达式为:![]() ;(2)点
;(2)点![]() 的坐标为:
的坐标为:![]() 或
或![]() ; (3)点
; (3)点![]() 的坐标为
的坐标为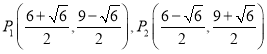 .
.
【解析】
(1)根据抛物线y=ax2+bx过A(5,0),B(1,4)两点,可以求得该抛物线的解析式;
(2) 过点![]() 作直线
作直线![]() 轴交
轴交![]() 点
点![]() ,设
,设![]() ,则
,则![]() ,分当点
,分当点![]() 在
在![]() 上方时和当点
上方时和当点![]() 在
在![]() 下方时,列方程求解即可;
下方时,列方程求解即可;
(3) 设![]() 交
交![]() 于点
于点![]() ,分当
,分当![]() 或
或![]() 时,由三角形相似,列方程求解即可.
时,由三角形相似,列方程求解即可.
(1)将点![]() 的坐标代入抛物线表达式,
的坐标代入抛物线表达式,
得:![]() ,
,
解得:![]() ,
,
所以抛物线的表达式为:![]()
(2)求得直线![]() 的表达式为:
的表达式为:![]() ;
;
过点![]() 作直线
作直线![]() 轴交
轴交![]() 点
点![]() ,如图,
,如图,
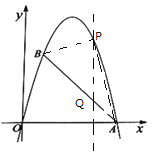
设![]() ,
,
则![]() .
.
当点![]() 在
在![]() 上方时,
上方时,
![]() ,
,
![]() ,
,
解得![]() ,
,
即![]()
当点![]() 在
在![]() 下方时,
下方时,
![]() ,
,
![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
即![]()
综上,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
(3)由(2)得直线![]() 的表达式为:
的表达式为:![]() ;
;
令![]() ,则
,则![]() ,
,
即直线![]() 交
交![]() 轴于点
轴于点![]() .
.
设![]() 交
交![]() 于点
于点![]() ,如图,
,如图,
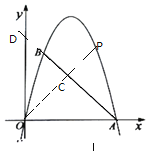
当![]() 或
或![]() 时,
时,
则![]() 分
分![]() 的面积为
的面积为![]()
![]() 轴交
轴交![]() 点
点![]() ,
,
![]() ,
,
![]() .
.
①当![]() 时,
时,![]() ,
,
由(2)得:![]() ,
,
即![]() ,
,
解得![]() ,
,
即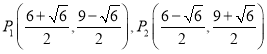 .
.
②当![]() 时,
时,![]() ,
,
由(2)得:![]() ,
,
即![]() ,所得方程无解.
,所得方程无解.
综上所述:点![]() 的坐标为
的坐标为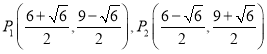 .
.


科目:初中数学 来源: 题型:
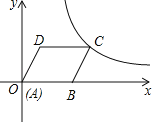
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y=![]() (k≠0)经过点C,则k的值为( )
(k≠0)经过点C,则k的值为( )
A.12B.15C.20D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
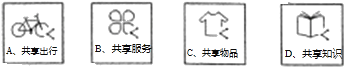
【题目】从共享单车、共享汽车等共享出行到共享充电宝、共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者,小宇上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),将这四张卡片背面朝上,洗匀放好.
(1)从中随机抽取一张,求刚好抽到“共享服务”的概率.
(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 位于
位于![]() 、
、![]() 之间,与
之间,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 点在
点在![]() 轴上方且横坐标小于5,则下列结论:①
轴上方且横坐标小于5,则下列结论:①![]() ;②
;②![]() ;③
;③![]() (其中
(其中![]() 为任意实数);④
为任意实数);④![]() ,其中正确的是( )
,其中正确的是( )
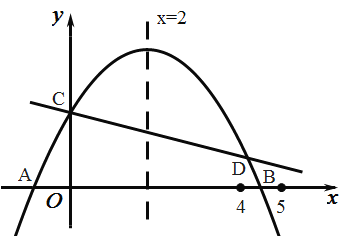
A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数y=x2﹣x﹣2的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的图形是函数y=|x2﹣x﹣2|的图象,已知过点D(0,4)的直线y=kx+4恰好与y=|x2﹣x﹣2|的图象只有三个交点,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
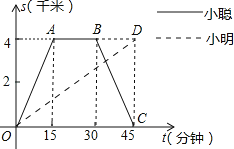
(1)小聪在超市购物的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,且OC=2OA,抛物线的对称轴x轴交于点D.
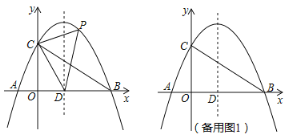
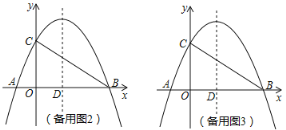
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上位于对称轴右侧的一个动点,设点P点的横坐标为m,且S△CDP=![]() S△ABC,求m的值;
S△ABC,求m的值;
(3)K是抛物线上一个动点,在平面直角坐标系中是否存在点H,使B、C、K、H为顶点的四边形成为矩形?若存在,直接写出点H的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com