
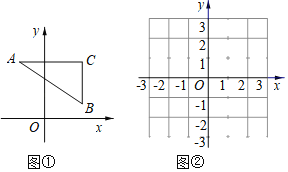
����Ŀ����ͼ������ƽ��ֱ������ϵ�У����߶�AB���������ֱʱ�����߶�ABΪб����Rt��ABC���ұ�BC��x�ᣬ���AC+BC��ֵΪ�߶�AB��ֱ�Ǿ��룬����L��AB�������߶�AB�������ᴹֱʱ���߶�AB��ֱ�Ǿ��벻���ڣ�
��1����ƽ��ֱ������ϵ�У�A��1��4����B��4��2������L��AB����
��2����ƽ��ֱ������ϵ�У���A������ԭ���غϣ���B��x��y������L��AB����2��
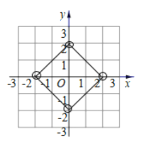
������B��x��y���ڵ�һ����ʱ����֪AC��x��BC��y����AC+BC��L��AB�����ɵ�y��x֮��ĺ�����ϵʽΪ�� ��������x��ȡֵ��Χ���� ������ͼ���л������������ͼ��
����ģ������˼�����̣��ֱ�̽����B�������������Σ���Ȼ��ͼ���зֱ���B�ڶ�������������ʱ��y��x�ĺ���ͼ����Ҫ��д��̽�����̣�
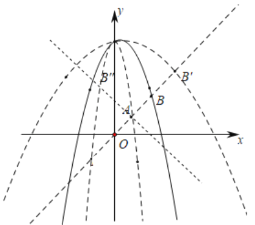
��3����ƽ��ֱ������ϵ�У���A��1��1������������y��a��x��h��2+5�ϴ��ڵ�B��ʹ��2��L��AB����4��
����a����![]() ʱ��ֱ��д��h��ȡֵ��Χ��
ʱ��ֱ��д��h��ȡֵ��Χ��
����h��0���ҡ�ABC�ǵ���ֱ��������ʱ��ֱ��д��a��ȡֵ��Χ��
���𰸡���1��5����2����y����x+2��0��x��2��ͼ�������������y��x+2��y����x��2��y��x��2��ͼ�������������3����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1�����ݶ���ֱ�Ӽ��㼴�ɣ�
��2������A(0��0)��B(x��y)���ҵ�B(x��y)�ڵ�һ���ޣ�L(AB)��2���ã�x+y��2���Ӷ��õ��𰸣�
�ڸ��ݵ�A��B���꼰��B�������ޣ�L(AB)��2�����������ۼ��ɵó��𰸻���ͼ�Σ�
��3����������������ʱ��Ӧ��h���![]() (x��h)2+5��1����x��h+4��x��h��4���ٷ�������ۣ���������ʽ������⼴�ɣ�
(x��h)2+5��1����x��h+4��x��h��4���ٷ�������ۣ���������ʽ������⼴�ɣ�
����![]() �ǵ���ֱ�������Σ���2��L(AB)��4����������㣬�ֱ���⼴�ɣ�
�ǵ���ֱ�������Σ���2��L(AB)��4����������㣬�ֱ���⼴�ɣ�
�⣺��1����A(1��4)��B(4��2)��
��L(AB)��AC+BC����4��1��+��4��2����5��
��2���١�A(0��0)��B(x��y)���ҵ�B�ڵ�һ���ޣ�L(AB)��2��
��x+y��2��
��y����x+2����0��x��2����ͼ����ͼ��ʾ��
�ʴ�Ϊ��y����x+2��0��x��2��
�ڵ�B�ڵڶ�����ʱ����x+y��2��
��y��x+2��ͼ����ͼ��ʾ��
��B�ڵ�������ʱ����x��y��2��
��y����x��2��ͼ����ͼ��ʾ��
��B�ڵ������ޣ�x��y��2��
��y��x��2��ͼ����ͼ��ʾ��
��3���ٵ���![]() (x��h)2+5��1ʱ��x��h+4��x��h��4��
(x��h)2+5��1ʱ��x��h+4��x��h��4��
��![]() ʱ����
ʱ����![]() ��
��![]() ʱ��2��L(AB)��4,
ʱ��2��L(AB)��4,
��![]() ʱ����
ʱ����![]() ��
��![]() ʱ��2��L(AB)��4,
ʱ��2��L(AB)��4,
��h��ȡֵ��ΧΪ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ڡ�![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��AC=BC��
�֡�L(AB)=AC+BC����2��L(AB)��4��
��1��AB��2��1��BC��2��
����ͼ���������߾���B(2��2)ʱ��L(A��B)��2����ʱ2��4a+5�����a��![]() ��
��
�������߾���B��(3��3)ʱ��L(A��B)��4����ʱ3��9a+5�����a��![]() ��
��
�������߾���B��(��1��3)ʱ��L(A��B)��4����ʱ3��a+5�����a����2��
�۲�ͼ���֪������������a��ֵΪ��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ܡ����п�����������Ŀ֮һ��ij��ѧΪ�˽���꼶ѧ�������ܡ�������������ȡ���־��꼶ѧ���������䳤�ܳɼ�������1000�ף�Ů��800�ף��������ܵ�ʱ��ij������η�ΪA��B��C��D�ĸ��ȼ�����ͳ�ƣ������Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
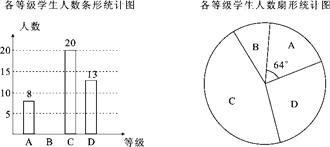
��1������ε����й���ȡ���� ��ѧ��������ͳ��ͼ�У�D������Ӧ������Բ�ĽǴ�СΪ ��
��2������ȡѧ�������ܡ����Գɼ�����λ�������� �ȼ���
��3������У���꼶����900��ѧ����������Ƹ�УC�ȼ���ѧ��Լ�ڶ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨѶ������Ѹ�ͷ�չ��������֮��Ĺ�ͨ��ʽ�����������ijУ��ѧ��ȤС�������������ϲ���Ĺ�ͨ��ʽ�������ʾ�(ÿ�˱�ѡ��ֻѡһ��)����ȫУ��Χ����������˲���ѧ������ͳ�ƽ������������������������ͳ��ͼ������ͼ����������Ϣ����������⣺
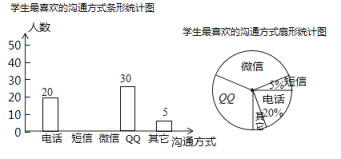
(1)���ͳ�ƹ�����˶�����ѧ��?������ͳ��ͼ�У���ʾ" ![]() "������Բ�ĽǵĶ����Ƕ��٣�
"������Բ�ĽǵĶ����Ƕ��٣�
(2)������ͳ��ͼ����������
(3)��У����1500��ѧ��������Ƹ�У��ϲ���� ���š����й�ͨ��ѧ����Լ�ж�����?
(4)ij��ס�������ͬѧ���������"��"![]() "�����绰"���ֹ�ͨ��ʽ��ѡһ�ַ�ʽ��Է���ϵ�������б�����״ͼ�ķ�������ס�������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ��ʣ�
"�����绰"���ֹ�ͨ��ʽ��ѡһ�ַ�ʽ��Է���ϵ�������б�����״ͼ�ķ�������ס�������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
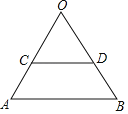
����Ŀ����ͼ����ABO���������Σ�CD��AB���ѡ�ABO�ơ�OCD������P��ת180��õ���EFG
��1����ͼ�л�����P�͡�EFG��������ͼ�ۼ�����Ҫ˵������
��2����AO��3![]() ��CD��2
��CD��2![]() ����A���˶���E��·���ij���
����A���˶���E��·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ�������ѳ�Ϊ������ϲ���Ľ�����ʽ֮һ��ͨ���ֻ����Լ������ߵIJ�������Ӧ���������ģ��Ա��ֻ����ݷ��֣�С����������330000�������IJ�����С�첽������300000�������IJ�����ͬ����֪С��ƽ��ÿ�����ĵ�������С��ƽ��ÿ�����ĵ�������3������С��ƽ��ÿ�����������Ŀ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ�
С��ͬѧ��������һ�����⣬��ͼ1��AB=AE����ABC=��EAD��AD=mAC����P���߶�BC�ϣ���ADE=��ADP+��ACB����![]() ��ֵ��
��ֵ��
С���о����֣�����BAM=��AED����BC�ڵ�M��ͨ������ȫ�������Σ����߶�BCת��Ϊ�ú�AD��ʽ�ӱ�ʾ�������Ӷ����![]() ��ֵ����ͼ2����
��ֵ����ͼ2����
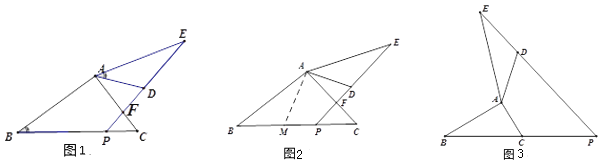
��1��С�������ȫ���������ǣ�_________��________��
��2�����㽫С�����о����̲��������������![]() ��ֵ��
��ֵ��
��3���ο�С��˼������ķ�����������⣺
��ͼ3������ԭ���С�AB=AE����Ϊ��AB=kAE��������P���߶�BC�ϡ���Ϊ����P���߶�BC���ӳ����ϡ��������������䣬����ACB=2������![]() ��ֵ��������ú�����k��m��ʽ�ӱ�ʾ����
��ֵ��������ú�����k��m��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
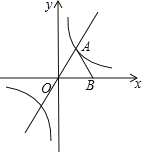
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У��ȱ�������OAB��һ����OB��x����������ϣ���A��˫����y��![]() ��k��0���ϣ����е�BΪ��2��0����
��k��0���ϣ����е�BΪ��2��0����
��1����k��ֵ����A������
��2����OAB��ֱ��OAƽ�ƣ�����Bǡ����˫������ʱ����ƽ�ƺ��A�Ķ�Ӧ��A�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
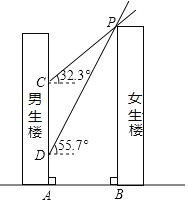
����Ŀ����ͼ������¥��Ů��¥����࣬��¥�߶Ⱦ�Ϊ90m��¥���ΪAB�����������磬̫��������ˮƽ�����ɵĽ�Ϊ![]() ��Ů��¥������¥ǽ���ϵ�Ӱ��ΪCA�����������磬̫��������ˮƽ�����ɵĽ�Ϊ
��Ů��¥������¥ǽ���ϵ�Ӱ��ΪCA�����������磬̫��������ˮƽ�����ɵĽ�Ϊ![]() ��Ů��¥������¥ǽ���ϵ�Ӱ��ΪDA����֪
��Ů��¥������¥ǽ���ϵ�Ӱ��ΪDA����֪![]() ��
��
![]() ��¥���AB��
��¥���AB��
![]() ������¥��30�㣬��߾�Ϊ3m����ͨ������˵�����ٲ����»��ܵ������Ӱ�죿
������¥��30�㣬��߾�Ϊ3m����ͨ������˵�����ٲ����»��ܵ������Ӱ�죿![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AOBC������ƽ��ֱ������ϵxOy�У���OA��y����������ϣ���OB��x����������ϣ������ߵĶ���ΪF���Գ��ύAC�ڵ�E���������߾�����A��0��2������C����D��3��0������AOB��ƽ������OE���������߶Գ�������ڵ�H������HF��
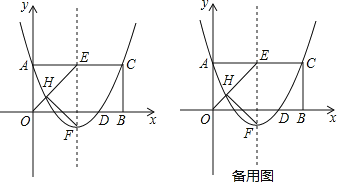
��1����������ߵĽ���ʽ��
��2����x�����ж���M���߶�BC���ж���N�����ı���EAMN���ܳ�����Сֵ��
��3�������������Ƿ���ڵ�P��ʹ���ı���EHFPΪƽ���ı��Σ�������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com