
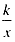 与直线y=
与直线y= 相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线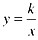 上的动点,过点B作BD∥y轴交x轴于点D,过N(0,-n)作NC∥x轴交双曲线
上的动点,过点B作BD∥y轴交x轴于点D,过N(0,-n)作NC∥x轴交双曲线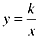 于点E,交BD于点C。
于点E,交BD于点C。
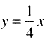 中,得y=-2,
中,得y=-2,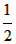 mn=
mn=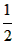 k,S△OEN=
k,S△OEN= mn=
mn=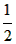 k,
k,

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源:第5章《反比例函数》中考题集(24):3、反比例函数的应用(解析版) 题型:解答题
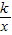 与直线y=
与直线y=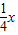 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=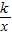 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=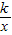 于点E,交BD于点C.
于点E,交BD于点C.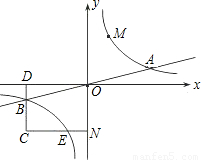
查看答案和解析>>
科目:初中数学 来源:2008-2009学年浙江省湖州市白雀学校九年级(上)期中数学试卷(解析版) 题型:填空题
 与直线y=
与直线y= 相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=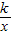 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=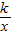 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2012年广东省广州市聚贤暨四中中考数学一模试卷(解析版) 题型:解答题
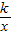 与直线y=
与直线y=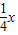 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=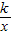 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=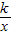 于点E,交BD于点C.
于点E,交BD于点C.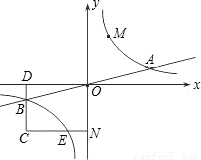
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《反比例函数》(05)(解析版) 题型:解答题
 与直线y=
与直线y=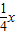 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=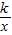 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=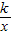 于点E,交BD于点C.
于点E,交BD于点C.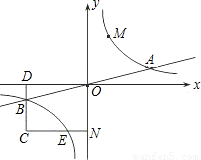
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(16)(解析版) 题型:解答题
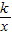 与直线y=
与直线y=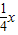 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=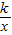 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=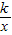 于点E,交BD于点C.
于点E,交BD于点C.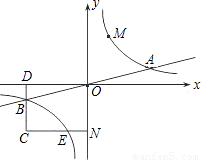
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com