
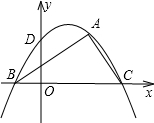
 坐标为(2,
坐标为(2, ),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D. ),
), ,∠ACF=60°,
,∠ACF=60°,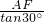 =3,
=3, =1,
=1,
 ,
, ,
, x2+
x2+ x+
x+ …
… x2+
x2+ x+
x+
 (x-1)2+
(x-1)2+ ,
, )可得AB所在直线的解析式为:y=
)可得AB所在直线的解析式为:y= x+
x+ ,…
,… ,
, ),
), +2…
+2… )其中O<t<3,
)其中O<t<3, )…
)…
 ×OC×PN+
×OC×PN+ ×OD×PG+
×OD×PG+ ×OB×OD
×OB×OD ×3×(-
×3×(- )+
)+ ×
× ×t+
×t+ ×1×
×1×
 …
… 时,四边形PDBC的面积最大,最大面积为
时,四边形PDBC的面积最大,最大面积为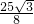 ,
, ,
,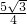 ).…
).… ),∠ABC=30°,利用直角三角形的性质,即可求得点B与C的坐标,然后利用待定系数法即可求得二次函数的解析式;
),∠ABC=30°,利用直角三角形的性质,即可求得点B与C的坐标,然后利用待定系数法即可求得二次函数的解析式; ),过点P分别向 x轴,y轴作垂线,垂足分别为N、G,由S四边形PDBC=S△POC+S△POD+S△BOD,即可求得答案.
),过点P分别向 x轴,y轴作垂线,垂足分别为N、G,由S四边形PDBC=S△POC+S△POD+S△BOD,即可求得答案.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
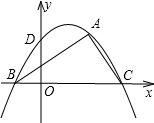 坐标为(2,
坐标为(2,| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年贵州省黔东南州正钰中学中考数学一模试卷(解析版) 题型:解答题
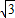 ),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
查看答案和解析>>
科目:初中数学 来源:2012年贵州省黔东南州凯里学院附中中考数学一模试卷(解析版) 题型:解答题
 ),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.
),∠ABC=30°,若抛物线y=ax2+bx+c恰好过A、B、C三点,且与y轴交于点D.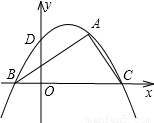
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com