
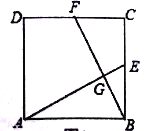
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,交点为
,交点为![]() . 若正方形的边长为
. 若正方形的边长为![]() .
.
(1)求证:![]() ;
;
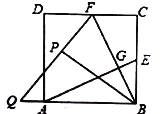
(2)将![]() 沿
沿![]() 对折,得到
对折,得到![]() (如图),延长
(如图),延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的长;
的长;
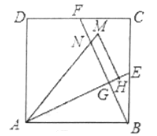
(3)将![]() 绕点
绕点![]() 逆时针方向旋转,使边
逆时针方向旋转,使边![]() 正好落在
正好落在![]() 上,得到
上,得到![]() (如图),若
(如图),若![]() 和
和![]() 相交于点
相交于点![]() ,求四边形
,求四边形![]() 面积.
面积.
【答案】(1)详见解析;(2)1;(3)四边形![]() 的面积是
的面积是![]() .
.
【解析】
(1)运用Rt△ABE≌Rt△BCF,再利用角的关系求得∠BGE=90°求证;
(2)△BCF沿BF对折,得到△BPF,利用角的关系证明QF=QB,在Rt△QPB中,利用勾股定理即可解决问题.
(3)先求出正方形的边长,再根据面积比等于相似边长比的平方,求得S△AGN=![]() ,再利用S四边形GHMN=S△AHM-S△AGN求解.
,再利用S四边形GHMN=S△AHM-S△AGN求解.
解:(1)证明:如图,
∵![]() 分别是正方形
分别是正方形![]() 边
边![]() 的中点,
的中点,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
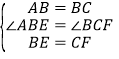 ,
,
∴![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:如图,根据题意得,![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
在![]() 中,设
中,设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)解:∵正方形边长为![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积是
的面积是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
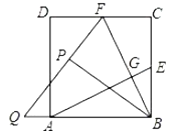
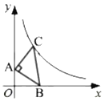
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一点,以
轴正半轴上一点,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,使
,使![]() ,点
,点![]() 在第一象限。若点
在第一象限。若点![]() 在函数
在函数![]() 的图象上,则
的图象上,则![]() 的面积为( )
的面积为( )
A. ![]() .B.
.B. ![]() .C.
.C. ![]() .D.
.D. ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
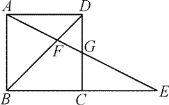
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(m+1)x+![]() (m2+1)=0.
(m2+1)=0.
(1)若该方程有实数根,求m的值.
(2)对于函数y1=x2-(m+1)x+![]() (m2+1),当x>1时,y1随着x的增大而增大.
(m2+1),当x>1时,y1随着x的增大而增大.
①求m的范围.
②若函数y2=2x+n与函数![]() 交于y轴上同一点,求n的最小值.
交于y轴上同一点,求n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() (a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
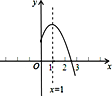
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“才饮长沙水,又食武昌鱼”.因一代伟人毛泽东的佳句,“鄂州武昌鱼”名扬天下.某网店专门销售某种品牌真空包装的武昌鱼熟食产品,成本为30元/盒,每天销售y(盒)与销售单价x(元)之间存在一次函数关系,如图所示.
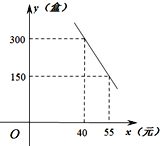
(1)求y与x之间的函数关系式;
(2)如果规定每天这种武昌鱼熟食产品的销售量不低于240盒,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3 600元,试确定这种武昌鱼熟食产品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
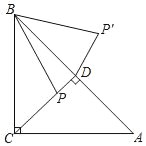
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com