
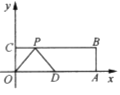
【题目】如图,在平面直角坐标系中,![]() 为原点,四边形
为原点,四边形![]() 是长方形,点
是长方形,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上运动,当
上运动,当![]() 是腰长为5的等腰三角形时,点
是腰长为5的等腰三角形时,点![]() 的坐标为_______.
的坐标为_______.
【答案】![]() 或
或![]() 或
或![]()
【解析】
题中没有指明△ODP的腰长与底分别是哪个边,故应该分情况进行分析,从而求得点P的坐标.
(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=![]() ,则P的坐标是(4,3).
,则P的坐标是(4,3).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
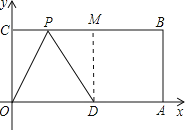
在直角△PDM中,PM=![]() =4,
=4,
当P在M的左边时,CP=5-4=1,则P的坐标是(1,3);
当P在M的右侧时,CP=5+4=9,则P的坐标是(9,3).
故P的坐标为:(4,3)或(1,3)或(9,3).
故答案为:(4,3)或(1,3)或(9,3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
x(元/件) | 38 | 36 | 34 | 32 | 30 | 28 | 26 |
t(件) | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
假定试销中每天的销售量t(件)与销售价x(元/件)之间满足一次函数.
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 、
、![]() 的垂直平分线相交于三角形内一点
的垂直平分线相交于三角形内一点![]() ,下列结论中,错误的是( )
,下列结论中,错误的是( )
A. 点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
B. ![]() 、
、![]() 、
、![]() 都是等腰三角形
都是等腰三角形
C. ![]()
D. 点![]() 到
到![]() 、
、![]() 、
、![]() 的距离相等
的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 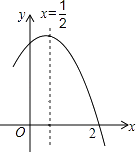
A.①②④
B.③④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
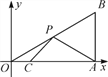
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=﹣ ![]() x+110(x≥0).
x+110(x≥0). 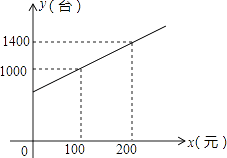
(1)在政府补贴政策实施后,求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式;
(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?
(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( ) 
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com