
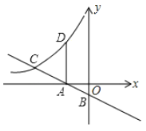
【题目】如图,直线![]() 与
与![]() ,
,![]() 两轴分别交于
两轴分别交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 图象在第二象限交于点
图象在第二象限交于点![]() .过点
.过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() ,若
,若![]() ,则点
,则点![]() 的纵坐标为__________.
的纵坐标为__________.
【答案】![]()
【解析】
作CH⊥x轴于H,如图,先利用一次函数解析式,确定B(0,-![]() ),A(-3,0),再利用三角函数的定义计算出∠OAB=30°,则∠CAH=30°,设D(-3,t),则AC=AD=t,接着表示出CH=
),A(-3,0),再利用三角函数的定义计算出∠OAB=30°,则∠CAH=30°,设D(-3,t),则AC=AD=t,接着表示出CH=![]() AC=
AC=![]() t,AH=
t,AH=![]() CH=
CH=![]() t得到C(
t得到C(![]() t,
t,![]() t),然后利用反比例函数图象上点的坐标特征得到(
t),然后利用反比例函数图象上点的坐标特征得到(![]() t)
t)![]() t=-3t,最后解方程即可.
t=-3t,最后解方程即可.
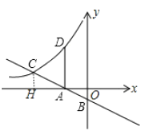
解:作CH⊥x轴于H,如图,
当x=0时,y=-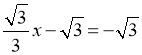 ,则B(0,-
,则B(0,-![]() ),
),
当y=0时,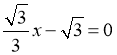 ,解得x=-3,则A(-3,0),
,解得x=-3,则A(-3,0),
∵tan∠OAB=![]() ,
,
∴∠OAB=30°,
∴∠CAH=30°,
设D(-3,t),则AC=AD=t,
在Rt△ACH中,CH=![]() AC=
AC=![]() t,AH=
t,AH=![]() CH=
CH=![]() t,
t,
∴C(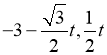 )
)
∵C、D两点在反比例函数图象上,
∴(![]() t)
t)
,解得t=![]() ,
,
即D点的纵坐标为![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
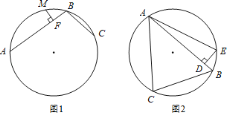
【题目】定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】换个角度看问题.
(原题重现)
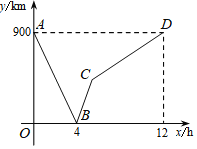
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
……
若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(问题再研)
若设慢车行驶的时间为x(h),慢车与甲地的距离为s1(km),第一列快车与甲地的距离为s2(km),第二列快车与甲地的距离为s3(km),根据原题中所给信息解决下列问题:
(1)在同一直角坐标系中,分别画出s1、s2与x之间的函数图象;
(2)求s3与x之间的函数表达式;
(3)求原题的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
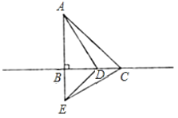
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连结
,连结![]() 、
、![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若点![]() 是
是![]() 的外心,当点
的外心,当点![]() 在直线
在直线![]() 的一个位置运动到另一个位置时,点
的一个位置运动到另一个位置时,点![]() 恰好在
恰好在![]() 的内部,请直接写出点
的内部,请直接写出点![]() 走过的距离为_____.
走过的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的正半轴上),与
轴的正半轴上),与![]() 轴交于点
轴交于点![]() ,矩形
,矩形![]() 的一条边
的一条边![]() 在线段
在线段![]() 上,顶点
上,顶点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上.
上.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
![]() 当矩形
当矩形![]() 的面积
的面积![]() 取最大值时,
取最大值时,
①求直线![]() 的解析式;
的解析式;
②在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,若点
,若点![]() 恰好落在该抛物线上,则
恰好落在该抛物线上,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
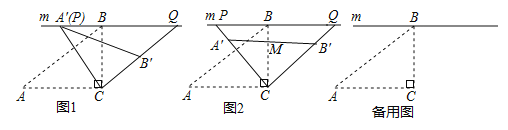
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() (点
(点![]() 的对应点分别是
的对应点分别是![]() ),射线
),射线![]() 分别交直线
分别交直线![]() 于点
于点![]() .
.
(1)问题发现:如图1所示,若![]() 与
与![]() 重合,则
重合,则![]() 的度数为_________________
的度数为_________________
(2)类比探究:如图2,所示,设![]() 与
与![]() 的交点为M,当M为
的交点为M,当M为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(3)拓展延伸:在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值,若存在,直接写出四边形
的面积是否存在最小值,若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由
的最小面积;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com