



科目:初中数学 来源: 题型:
 附加题:
附加题:| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
| 2006 |
| 2007 |
| 2006 |
| 2007 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 99 |
| 1 |
| 98 |
| 1 |
| 100 |
| 1 |
| 99 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
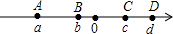 如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.
如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知|a-2|+|b+6|=0,则a+b=______.
(1)已知|a-2|+|b+6|=0,则a+b=______. ,
, ,
, ,将以上三个等式相加得:
,将以上三个等式相加得: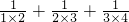 =1-
=1- +
+ -
- +
+ -
- =1-
=1- =
= .
. =______.
=______.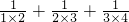 +…+
+…+ =______.
=______. -1|+|
-1|+| -
- |+…+|
|+…+| -
- |+|
|+| -
- |的值.
|的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com